The Phase Vocoder - Part II
Introduction
In our Part 1 of this phase vocoder tutorial, we saw how to create a basic phase vocoder for time-stretching. While it is by no means a simple MSP patch, it is a useful one. In addition to time-stretching, the phase vocoder has been used for transposition and "freeze" effects, which we will be discussing in this article. If you are unfamiliar with the phase vocoder principle, we suggest you review Part I of this series of articles. Additionally, if you are unfamiliar with Fast Fourier Transform (FFT) you may wish to familiarize yourself with MSP Tutorial 25 (about FFT and the fft~ object) and MSP Tutorial 26 (about the pfft~ object).
In Part 1 of this tutorial, we designed two phase vocoder patches - one which works with polar coordinates (amplitude and phase values), and one which works with cartesian (x, y) coordinates. While the former is easier to understand (and simpler to patch together), the latter is more efficient, since it avoids using trigonometric math functions (specifically the arctan function), which are computationally expensive. We will take our existing phase vocoder patch as a starting point, and show our modifications to both the polar and cartesian versions.
Transposition
For many years in the first few decades of digital synthesis, the most convincing method of transposing a sound without changing its duration was to use a phase vocoder. In fact, using a phase vocoder you can change both the transposition and speed independently - so, for example, you could transpose a sound and octave higher while playing it back twice as slow!! Performing a transposition with the phase vocoder involves only a few changes to the buffer~-reading part of the patch.
The first change is the addition of a 3rd inlet to our pfft~ subpatch so we can control the transposition. As with the time stretch inlet, we also use a sample and hold (sah~) object to make sure the transposition value is held constant for all bins in our FFT. Since transposition involves reading a larger or smaller chunk of sound from our buffer~, we scale the output of the counter~ by the transposition factor before we add it to our sample offset into the buffer~. If our transposition factor is greater than one, we will be reading a larger window from the buffer~ albeit at a faster speed. Conversely, if the transposition factor is smaller than one, we will be reading a smaller chunk of the buffer~ at a slower speed.
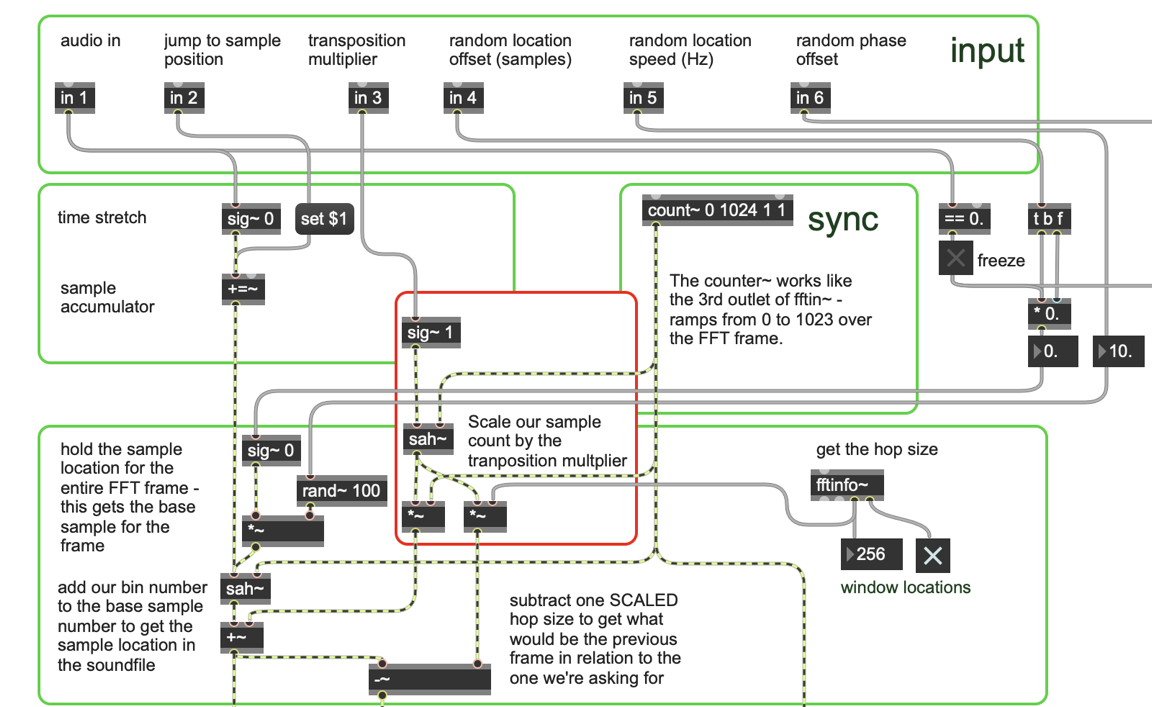
One other change we need to make is to replace index~ with play~. Since the index~ object does not interpolate sample values, we will degrade the quality of the sound if we use it. The play~ object uses 4-point interpolation to read "fractional samples" from the buffer~, so its output will sound better when we read the buffer~ at faster or slower speeds. Since the play~ object takes millisecond values instead of sample values as input, we need to add a sampstoms~ object to convert the samples to milliseconds and read the proper size chunk of sound from our buffer~.
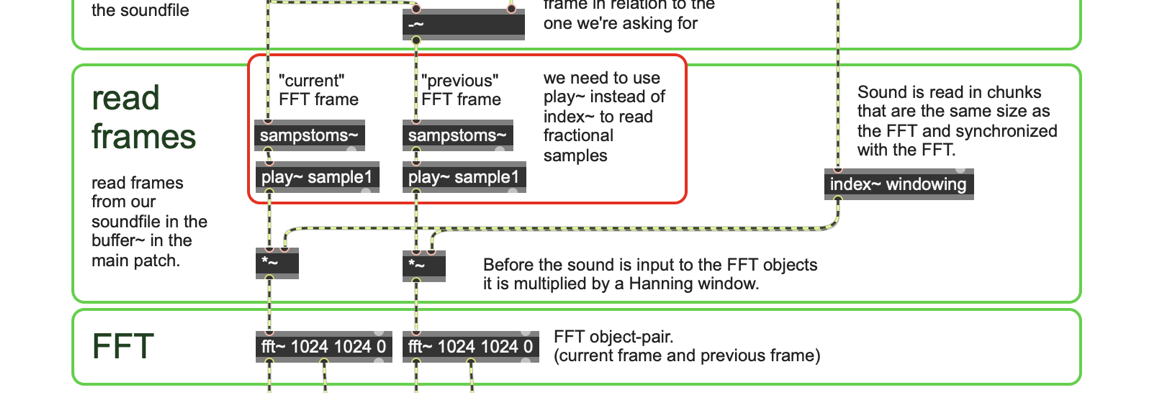
Putting it all together, we can use this transposition for both the polar and cartesian patches, since these changes do not affect the actual phase vocoder part of the patch.
One other important change we are making to the cartesian patch is to use a unique number for the send~ and receive~ name. We do this by beginning the name with a #0 which will be replaced with a different number in each instance (This is described here). It lets us have multiple phase vocoder patches open at once without the send/receive names interfering with one another.

Note that for both patches we make use of the "args" possibility for pfft~. Following the 5th argument to the pfft~, note the word "args" and the FFT size. This is convenient for allowing you to change the FFT sizes for the fft~ and ifft~ objects in the pfft~ subpatch. (If you do change the FFT size, make sure to change the size of the windowing function in the message box below the loadbang, and double-click the loadbang to recalculate the window function at the new size.) Also, you might want to refer to the "Time vs. Frequency Resolution" technical detail in MSP Tutorial 26, since different sounds might work better with different FFT sizes.

Freeze Effect
Although we can set the playback speed to zero, and thus "freeze" the sound at a certain point in time, the effect is rather static and mechanical. We can enliven our freeze effect by adding two things to our patch - some random variance in the playback location, and some additional small random variance in the phase. Together they produce a much better freeze effect than can be achieved without them.
Here's what we need to do:
First, we need to only activate our freeze parameters when the playback speed is set to zero. Since our first inlet to the pfft~ subpatch is the user-defined playback speed, we can simply check this value in order to activate our additional freeze parameters.
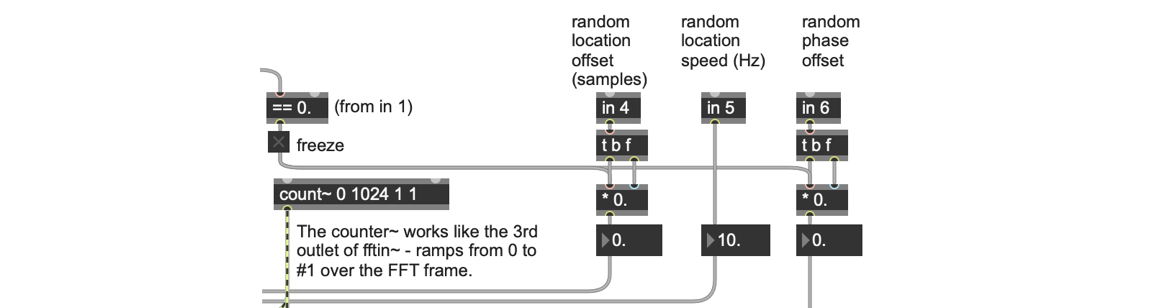
Next, we can use the rand~ object to randomly oscillate the buffer~ read location around the given playback location. We can control both the oscillation speed (with a frequency to rand~) and the oscillation depth - which is our random playback location variance (with a signal multiply). Using just this technique automatically enlivens the frozen sound.
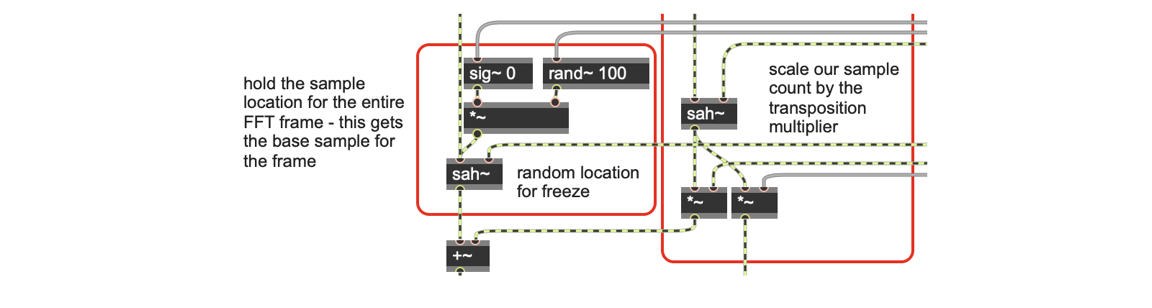
Finally, we can add a very small amount of random phase deviation to the bins of our spectrum. Generally this is something we try to avoid in a phase vocoder, because it adds strange audio artifacts to our sound; however, in the case of a freeze, a very small amount of phase deviation from bin to bin actually breaks the mechanical sound of the freeze!
In our polar coordinate phase vocoder adding the phase is straightforward - we simply add low volume white noise to our phase component.

However in the cartesian coordinate version of the patch things become slightly more complicated. We have to create a complex signal whose phase component has the noise in it, and perform a complex multiplication to rotate the phases. (Phase rotation via complex multiplication and division is explained in Part 1 of this phase vocoder tutorial) To achieve this we use two cycle~ objects whose phase is 90 degrees apart to represent the sine and cosine components of the complex signal, and control their phase input directly with the white noise. We're using our complex multiply subpatch, used elsewhere in the phase vocoder, to add the phase deviation to our complex signal.
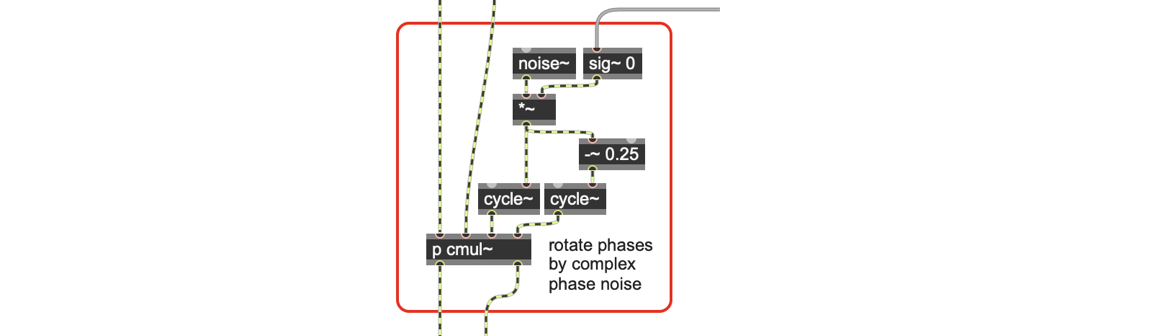
Our cartesian phase vocoder now looks like this:
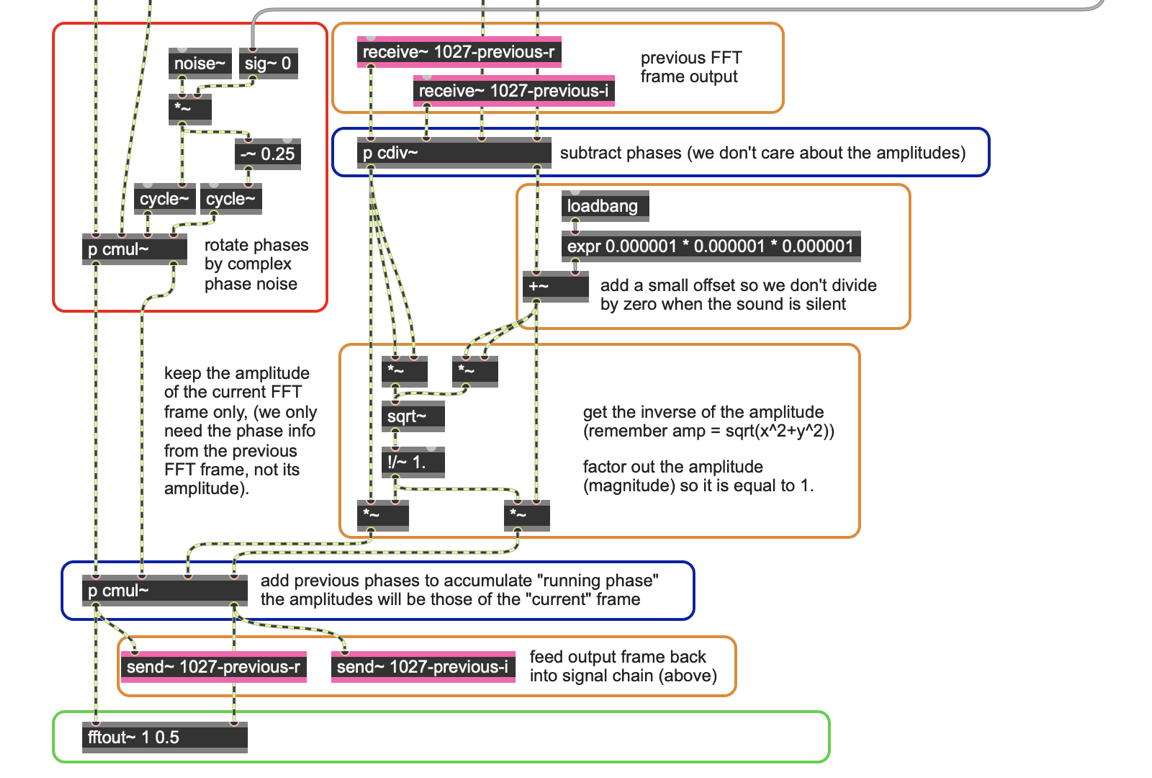
It is quite a bit more complicated than the equivalent polar version shown in Figure 7, but you will notice that, as with the simple cartesian version shown in Part 1 of the phase vocoder tutorial, it is markedly more efficient. For complete views of these patches, we suggest opening up the patches themselves in Max/MSP and trying them out!
Conclusion
With these additions to the phase vocoder we can control a sound's playback speed and transposition independently of each other, as well as "freeze" the sound with a bit of added liveliness. We have also improved the patch so we can provide arguments to the pfft~ subpatcher in order to change the FFT size of the fft~ and ifft~ objects that we must use to read the sound from the buffer~.
by Richard DudasCort Lippe on July 2, 2007

