[modulo] ?
hello
I am looking for an equivalent of the [modulo] object (of puredata) in maxmsp
the modulo is a math operator a bit equivalent to % instead that with negative value it doesn't output the same thing:
(e.g. if I want [modulo 33] of -1 give 0 and [modulo 33] of -2 give 32 [modulo 33] of -33 give 1)
As far as I know puredata has a [mod] operator equivalent to % in Max.
Can you point to some definition/documentation of your [modulo] object?
sorry I mean the [mod] object
and [%] doesn't handle negatives value in the same way [mod] does
But there should be a proper documentation how [mod] handles negative values.
What you describe looks rather strange to me..
from pd documentation :
[mod] takes a number in its left inlet and will divide that number by either the creation argument or the number given at its left inlet and will produce the value of the remainder at its outlet. If no creation argument is given, then the default value is 1
(nothing about negative values)
use expr?
yes
The Max [%] object handles modulo exactly the way most C implementations do, which is mathematically incorrect.
[expr] may do the trick, otherwise hang a [if $i1 >= 0 then $i1 else out2 $i1] after the [mod] object. Hang a [+] object after the if's second outlet, make sure the [+] operand is set to your modulo. Et voilà!
Interesting. So does pd have a mathematically correct implementation of modulo?
"Boute argues that Euclidean division is superior to the other ones in terms of regularity and useful mathematical properties, although floored division, promoted by Knuth, is also a good definition. Despite its widespread use, truncated division is shown to be inferior to the other definitions."
pd (apparently) uses Euclidean, max truncated division.
Time for an attribute?
Thanks for the link. Euclidean modulo seems useful in practice (eg. result is always positive).
So based on the article I've made an abstraction for usage in Max.
Here's an additional patch for flipping direction across a dividend input of zero, along with a question:
Might there be a more efficient method of achieving ^this result?
The gen world has [wrap], which implements euclidean modulo. You could use gen~, gen, jit.gen etc. as needed according to the kind of data.
@Graham; Oh wow, nice. :)
For whatever reason, I'd been putting off getting into gen, but after this, I'll be burrowing deep into this.
If you have any other suggestions for further optimizations, here's the current abstraction:
Again. Thank you so much.
Edit: Actually, [wrap] seems to shift from 0-2 to 1-3 an iteration after the dividend goes negative. I'm not sure where this is going wrong, nor do I have any clue as to how to fix it. =/
What about the [pong] object?
Same thing, I'm afraid. =/
One iteration after the dividend goes negative and the range shifts from (0 to N-1) to (N - 1)
[110.loopi]
expr ((($i1%$i2) + ($i2)*(($i1%$i2)==0))*($i1>=0)) + ((((($i1%$i2)+$i2) + (-$i2)*((($i1%$i2)+$i2)==0))*($i1<0)))
[110.loopf]
expr ((($f1-int($f1/$f2)*$f2) + ($f2)*(($f1-int($f1/$f2)*$f2)==0))*($f1>=0)) + ((((($f1-int($f1/$f2)*$f2)+$f2) + (-$f2)*((($f1-int($f1/$f2)*$f2)+$f2)==0))*($f1<0)))
Yes, I see the issue with [pong]
A three-object solution then:
how about this abstraction?
Instantiate as: [modulo 5] for example...
Apologies for the delay.
@Luigi: This seems to do exactly what I was looking for. :)
@Roman; I've been looking at both of your expressions and something interesting is that:
1. Regarding both: With a dividend input of zero, the divisor still increments the output.
2 . Regarding [110.loopf]: With a divisor input of zero, the dividend still increments the result.
I'm just curious what the benefit/ reasoning of each are?
Many thanks to everyone for the help. <3
back in the days i´ve never been so sure about what "fold" and "wrap" actually is, and how to make it, and there was no non-MSP [pong] object either.
even worse, expr took %, but still couldnt do float, just as the % object.
loopi´s purpose is to wrap numbers as if the negative range and 0 would be positive numbers. which is not the same as ignoring the sign. ;)
it will always output a range of 1-n, where n+1 = 1, and 0 is n again, so that it continously wraps no matter if the input is below or above the output range.
as a result, for example my sequencers can take negative numbers as time values. (where otherwise a simple [%] would be enough.)
"-4"
loopi 16
"13"
that output range of 1-n is probably what it is all about.
the float version was made just for fun. i think it could be optimised but i never found out how. try 0.03 and 1.5
yes, the argument should be 1 or higher. an arugment of 0 would default to 16 in my abstraction.
The other old trick is to use double modulo:
@Roman -- re: "as if the negative range and 0 would be positive numbers" - It's funny; I'd actually been considering popping off trig 16 on my Elektrons, and shifting everything over by one for ease of converting patterns written at 1x speed to 1/2x speed utilizing microtimings (for extending phrases). Instead I went ahead and built a calculator in Max, but the point being, I do believe I can appreciate the thought process behind ^this. :)
I especially appreciate the inclusion of the float variant, because I can imagine how long that must have taken you to arrive at that solve.
@KLSDIZ: Ok, that's pretty damn slick, lmao. Thanks for sharing, man.
@Roman (whom I've come to consider the "expr syntax wizard"): I wonder if you could either assist in adapting this to expr/ vexpr syntax, or maybe have any pointers to share in doing so.
The purpose it serves is to flip the value across a matrix, when given a negative dimension input.
(IE. With a dimension input of 5, the range is (0, 1, 2, 3, 4). With a dimension input of -5, the range is (5, 6, 7, 8, 4), which when followed with a modulo/ wrap gives you (4, 0, 1, 2, 3))
Not with expr, but it looks like this does the same with less objects?
not sure if it is right ... but i doesnt make too much sense anway. :)
t b i
expr ($i1<0) * (abs((abs(((abs(($i1%$i2)-$i2+1))%$i2))+$i2)))%1 + ($i1>=0) * ($i1%$i2)
Thanks, Jean. :) -- It would seem that replacing the final [%] with the [p eumodulo] from my patch does do exactly the same thing. (The issue it fixed was that it was reversing direction after the first iteration after going negative.)
The reason for seeking vexpr syntax is that I'd like to operate on a list using vexpr's "@scalarmode 1", rather than operating on each value, individually.
@Roman; Haha, I believe that's close, but not quite. My apologies; I believe I was unclear. Let me try and simplify.
The desired behavior is:
1. If $i2 > 0, then wrap from 0 to $i2-1 (ie. if $i2 = 5, then -9 = 1, -5 = 0, -1 = 4, 1 = 1, 5 = 0)
2. If $i2 < 0, then wrap from $i2-1 to 0 (ie. if $i2 = -5, then -9 = 0, -5 = 4, -1 = 3, 1 = 0, 5 = 4)
@KLSDIZ -- This is legitimately incredible/ elegant work, man. This is way simpler than I was expecting. (Idky I was expecting need to use at least one boolean operator.)
Thank you so much. <3
cheers! 🥂
well, ONE comparison operator is still present in the first half; why the other one is not needed that the usual trickery between logical operations and arithmetics. :)
sometimes you write if a then * x + if not a then * y and then you read what you wrote and find out that it can be shortened because you somewhere do + 0
with similar tricks you sometimes also can have 3 or more conditions in a single expr.
@KLSDIZ: Cheers, indeed. 😊
@Roman: Haha, yeah. Seeing the solve was a bit of a lightbulb moment; Idky, but I doubt I'd have arrived at that on my own -- well, at least in a reasonable time frame. 😅
- take jfc´s patch
- exchange all objects with expr´s
- now insert them into each other from bottom to top
after you did that 20 times with complex patches, you speak expr fluently.
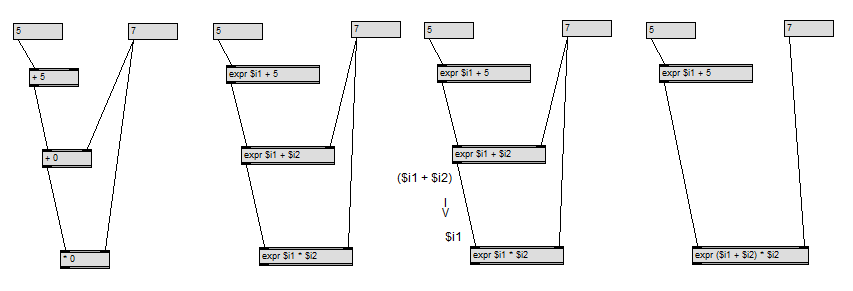
@Roman: Thanks, man. ^this makes total sense. :)
max, min, random, int and a few other basic objects are easy to replace, too.
even a few which arent so obvious. :)
[clip] -> expr max(min(a,b),c)
[split] -> basically the same as if then else out2 or [gate 2], so you can use > and <=
for [mtof] there are three solutions, one of them should be in the help file, same with [atodb].
...
when you combine conditions like
expr ($f1>100.) * (($f1/5)<1000.) * 5
(if input is greater 100 and input/5 smaller than 1000 then output 5 else 0)
you can use logical-and like in [if]
expr ( ($f1>100.) && (($f1/5)<1000.) )* 5
but note the additional brackets.
...
i have yet to replace jit.pwindow and kink~ using expr, but maybe one day.
@Roman: Thank you so much for this. -- I wish you could bookmark posts, so I've now screenshot ^these with plans to print/ laminate. 🙂
Aaron
somewhat shorter version, just for reference.
old thread, dont reply.
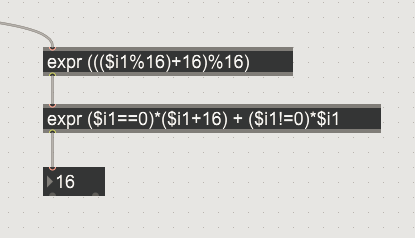
Hey there, I'm currently trying to implement a floor value to a modulo wrap in vexpr (for use with lists). I feel like I'm getting close to the solve, but I'm feeling a bit fatigued atm and am curious if anyone might have a simpler approach. (ie. an input value of 5, with a ceiling value of 4, and a floor value of 2, would give an output of 3, etc.)
