An MC Journey, Part 2

Welcome to the second part of a short tutorial series that’s something of a departure for me in that it’s personal and idiosyncratic. As a Max user, I expect that, like me, you make your way through the Package Manager or follow up on Forum postings or haunt the Projects - or just type what you’re interested in into the Search on any patcher window to see what comes up every once in a while - and then you start spelunking. I know that lots of people do it because the Forum is full of people who are obviously in the midst of just that; and when you think of it, the Projects section of the website and the Package Manager are full of people sharing what they found while they were out working in the Patch Pile.

So when someone asked me about writing an MC tutorial, I thought I might try something a little different: I’d try to put together a little homage to the many Max users out there who’ve taken some new Max feature of set of tools and tried to figure out what to do with them that fit their own interests. There’s an element of risk in this — namely, that there’ll be readers who wonder why on earth something I’m doing would matter at all. But we’re all like that, aren’t we?

A Step Sideways

In my last toe-in-the-water venture into MC-land, I started with something I use all the time – Low Frequency Oscillators (LFOs), and quickly discovered that a lot of the extra messaging and logic necessary to control them could be really easily replaced using MC. It was a great first step, and I’m using the results regularly now.

While I was hunting around for ways to generate some variety in a less stochastic way than using the deviate message, I happened across a trio of messages I could use in an MC patch to spread a set of values out between a low and a high range: spread, spreadinclusive, and spreadexclusive.

To get a feel for how the messages worked, I set up a simple Max patch that let me enter a range and compare the results for several variations of the spread messages in one place at one time. Here’s the spreading.maxpat patch in action (I’ve included it in the tutorial patches this time out so you don’t need to hunt for it or download it again):

As I stared at the different outputs, a little light went on, and my trip down this tutorial’s rabbit hole started in earnest: I suddenly realized that some of those numbers looked awfully familiar somehow. Then I saw it —those values could be used to specify oscillator frequencies!

My artistic practice for many years has involved electronic work that combines some features of central Javanese gamelan music with non-equal-tempered tunings and timbres. That means that I work with scales whose notes are not in the same positions as you’d find on a regular keyboard. As a practical matter, I started using something called Just Intonation to define what those scales were. Simply put, Just Intonation lays out pitches in a scale by using small whole number ratios rather than the twelfth root of 2 as a frequency multiplier that your regular equally tempered piano uses. Another big part of the reason that Just Intonation was an appealing choice also had to do with the fact that frequency ratios are the means by which you can control the pitch of sidebands in a frequency-modulated oscillator. Long experience in both these areas is probably the reason I saw those lists of spread numerical values and thought “chords!”

The MC patch I was staring at could be repurposed as an MC patch that would output audio whose intervallic structure could be defined and changed on the fly.

Tuning and Timbre (A Quick Overview)

If you’re not really familiar with things like Just Intonation and tuning, let’s start with a really simple patch (00_consonance_sweep).

Open the patch, click on the ezdac~ object, click on the red box, and listen. You’ll hear two oscillators that slowly go out of tune with each other so that one of them slowly sweeps upward until it’s an octave higher in pitch. Along with way, you’ll hear the two oscillators beating against each other, and you’ll also notice that there will be points when the beating quiets or when you momentarily recognize intervals you know. It turns out there’s a pattern to that sliding or alignment between the two pitches (and you might try them using waveforms other than sine waves, while you’re at it), and there's a name for what you're hearing. Psychacousticians such as Ernst Terhardt refer to it as dyadic harmonic entropy - an experimentally-derived map of how listeners perceive the relative consonance or dissonance of two notes sounding together.

There's unison on the left, and a pair of pitches an octave apart on the right. Those bumps in between the highly consonant and ending points refer to pitch ratios that we hear as consonant. The big dip toward the middle is a pitch ratio of 2 to 3 (which is a perfect fifth). You'll find some other bumps you'll probably recognize: 3 to 4 (a perfect fourth), 4 to 5 (a perfect third) and 5 to 6 (a minor third). The deeper the "bump," the more consonant the interval seems.

But I'd actually heard about that a very long time ago, and from an unlikely place - from Donald Duck. This happened a long time before I ever knew what Equal Temperament was, let alone what the relationship between whole number ratios and pitches were. Go on - scroll ahead to 2:30 or so in this video and enjoy!

And what you just listened through in that last MSP patch has one other interesting property: the perception of consonance is also related to the harmonic overtone series. The perception of an interval's consonance varies according to the number of overtones coincide with each other.

Here's an example that shows how the harmonic series of two notes a perfect fifth apart (i.e. in a frequency relation of 2 to 3) versus two notes a major whole-tone apart have overlapping harmonics (shown in blue).

So I decided to use these ideas to create a set of drones where the harmonic content of an individual "note" was related to the frequencies in my "chords" using MC.

Numbers, Fractions, and Musical Intervals

When I first started working with non-12-tone-equal-temperament (or !12tET, as it's sometimes called), it was difficult to remember my intervals. I knew that 1:1 was unison, and 2:3 was a perfect fifth above that, and 1:2 was an octave, but the rest of pretty tough to remember. And when it came to harmonics, the process of multiplying frequencies and then folding the result so that they fell into the compass of a single octave (instead of being 16 octaves above the original note) was quite a lot of work.

Happily, composer and microtonal theorist Kyle Gann came to my rescue with his helpful Anatomy of an Octave web page, chock-full of useful descriptions of ratios and the names we usually associate with them. That work, in turn, is based on Alain Danielou's encyclopedic Comparative Table of Musical Intervals, which has been out of print for quite a while. (You can find a link to a PDF here, should you be interested.)

I took his table as my starting place, and made a few judicious changes:

• I removed the references to Equal temperament from the table.

• I'm working with decimal values as output from the spread, spreadinclusive and spreadexclusive messages, so I've calculated and included the floating-point decimal equivalents of each ratio in the table listing.

The document Interval_Aid.pdf contains the fruit of my labors, and I've included a copy of it with the software download. I hope you find it useful.

Armed with these tools, I decided to redo my original spreading.maxpat patch so that I had a single output source for all of the spread message variants:

Exploring the spread message results involved little more than inputting the upper and lower range and consulting my Interval_Aid document.

In this case, the result was a chord consisting of a root, a perfect major third, a perfect fifth, and a perfect minor seventh. Not too bad!

For upper limits higher than 2.0, it's just a matter of halving the results until they fall within the 0. - 1.0 range and then consulting the table.

This gives us a chord consisting of a root, a perfect minor seventh, a perfect major third above that, and an overtone 6th (3.25 * .5 to check the interval). It's a lot easier to listen than to look up stuff, so I wired together a little bit of MC to generate a separate waveform output for each of those frequency ratios (with a selectable frequency for the root tone, of course). The result of my spread message modifications and the MC necessary to generate the four outputs is straight-ahead basic MC that you've seen in any number of online/video tutorials (and which you'll recognize from techniques in the first installment of this tutorial). Here's the result: the 01_make_me_a_chord.maxpat file.

Remember how I mentioned the term "rabbit hole?" This is it, in a nutshell — lots of time exploring spreads and figuring out what intervals I was actually hearing, adjusting the upper limit so that the third value showed up in the second position and listening to that, and so on... .

From Timbre to Tuning

The world provides us with interesting examples of musical practice where an exotic tuning can be partially explained by looking carefully at the timbre of the instrument playing the scale. In his book Tuning, Timbre, Spectrum, Scale, William Sethares approaches the idea of sensory consonance from a slightly different angle: what if we base the notes in our scale on the timbre of an instrument to maximize the harmonic overlap?

For me, that was an obvious next step, and one that wasn't all that difficult to achieve. Here's what I needed:

• Grab each of the four values that resulted from the spread

• Use those four values to set the "offset from root" frequency for each note — that way, the notes in the "chord" precisely match the position of the four "partials" of the root note

• Output the 4 results as stereo audio, and combine those signals together

After my LFO adventure described in part 1 of this tutorial series, making that happen was just a question of copying my basic patch 4 times and adding a few judicious MC versions of MSP objects I knew well:

• mc.unpack~ 4 to give me the frequency multipliers for each note in the "chord"

• an mc.*~ object for each of the unpacked note values to use alongside my base frequency multiplier

• a little mixdown at the end with a quartet of mc.mixdown~ 2 objects to spread my partials to stereo

• a final mc.combine~ 4 object to game them for a final mx.mixdown~ 2 for stereo mixdown:

What's the result of linking the collection of spread pitch values to the base frequency of each of the four stereo note outputs? Let's take a look at the frequency outputs for each of the four "partials" of the four notes in our "chord." In this really simple case we'll use 1. and 4. for the spread values, and use spreadinclusive $1 $2 to set the output range, and set a base (root) frequency value to 100. Hz.

This is about the simplest case you can imagine, but you'll already see what's going on here: Since frequency is exponential (each doubling of frequency is an octave), you'll notice a proliferation of octaves from the 100 Hz. base, shown in black, spread over 5 octaves. The notes in blue divide down to ratios of 2:3, which also gives us 3 octaves of pitches a perfect fifth up from the base frequency value.

Let's look at slightly more exotic case. We'll use 1. and 2. for the spread values, and use spreadinclusive $1 $2 to set the output range, and set a base (root) frequency value to 100. Hz.

This time, things are a little denser and stranger. We've still got three octaves of our base pitch of 100., but the spread has given us two non-octave intervals, which you can see in the first column: 1.3333, which is a perfect 4th (show in blue, along with its octave variants), and 166.67 (shown in red with its octave variants) which is a major 6th in Just Intonation (3:5). If you're a serious Just Intonation fan, you'll also notice the minor seconds (10:11 or 222.22 as shown here) and a minor seventh in there, too (9:16 or 177.78).

Setting things up this way pretty much guarantees that there will be pitches that emerge from the mass of notes because the partial structure and the scale notes themselves are related.

While it might be interesting to look at the numbers, that's not what I use the patch for.

I learn by going where to go. No, really.

I choose two values and a spread variation and then grab one floating-point number box or the other and then scroll it until I can hear something emerge from the sprawl of frequencies. Occasionally, I use the line object to set up a sequence of slow transitions from one of those discovered emergences to another and lay them atop a drone bed derived from the same base frequency, too. It's been a surprising source of raw material that I would never have happened upon without MC.

Stirring the Cauldron

I've been using the mc.mixdown~ object all along to handle transformations from one channel grouping to another (as well as handling the final step of folding down to a stereo output). In the course of reading up on the object, I happened upon the description of how I could use this handy object for panning as well as mixdown — you can read up on it in the Mixing and Panning in MC section of the documentation. The implementation is really well thought-out and varied enough that I found one mode that made intuitive sense to me right away: Mode 0 (0.- 1. - circular panning).

Simply put, you set pan position as a value between 0. and 1.0 that represents an even-power pan within a circular configuration of channels spread evenly across that range. Here's what a four-channel mono configuration looks like:

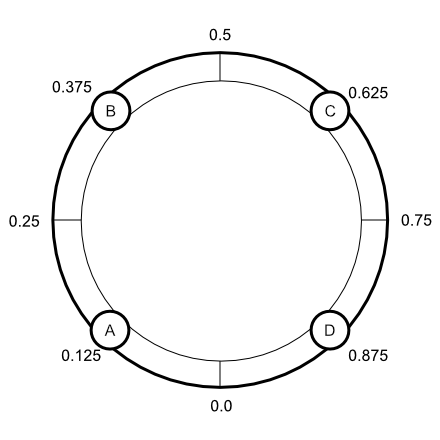
That looked like just the thing, with one minor variation: I had four stereo channels to spread across the panning field rather than four mono channels. While I could certainly use position C in the example for the right channel of my first stereo pair whose location was at point A, I thought it might be more interesting to be able to locate the starting point for all eight signals and individually and then use a single source to rotate them all. (I may decide to go with separate rates for each channel someday, but what I've got now works just fine for me.)

Given the complexity of what was being managed, the setup for circular panning was surprisingly simple: send a list that identifies the pan positions for each channel to be mixed down to the right inlet of the mc.mixdown~ object. That's it. Want to move things around? Just add some patching that modifies those positions in the list, and you're done.

Once again, the MC extensions of standard MSP objects I use all the time saved the day. I set up some patching in MC style to

• locate the audio channels in the stereo field

• animate them by simply adding the output of an mc.rate~-scaled mc.phasor~ object to those audio channel location's list items

• wrap those resulting sums around the range 0. - 1.0 using mc.pong~ 1 0. 1. object.

I couldn't believe how simple it all was - I set the phasor~-driven stuff up, added the patching that sets the channel positions, connected the wrapped output to an mc.mixdown~ object's right inlet, and that was it.

Here's what that portion of the 03_stir_my_drone.maxpat patch looks like:

The cool part of this patching is there I can easily modify it to provide separate rates for each of the phasors used to set the pan positions, and I can arbitrarily space the stereo pairs at any distance I want (you'll notice that this patch locates the first pair at .125 and .75, and placed the other channels in a similar relation to one another).

Well, I think that's enough possible exploration for now. There are still a number of interesting things I could add that occurred to me along the way:

• Having all of my "partials" at the same amplitude doesn't really resemble what real-world timbres in their steady state look like, but I can use my trusty spread message to modify the amplitudes of the individual "partials" for a more realistic and subtle result.

• The number of partials/pitches in my patch is completely arbitrary. Working with only 3 instances will more regularly give me something that resembles a chord. Alternately, I can use more than 4 instances and explore scales where the pitches are defined by using the same denominators — a 5-tone scale which uses pitches placed at 1.0 or 1/1, 1.2 or 6/5, 1.4 or 7/5, 1.6 or 8/5, and 1.8 or 9/5, for example).

• As long as I'm at it, why not use those spread messages to set the positions in the stereo field?

Anyhow, I hope that you can find something interesting to explore in the midst of my own idiosyncratic investigations recorded here. Please enjoy this responsibly.

Learn More: See all the articles in this series