Representing scales, chord shapes, inversions etc. in MAX
Hello,
is there an agreed-upon and/or recommended way to work with representations of scales, chord shapes, inversions and the like in MAX projects? Background: I'm working on a project for MIDI guitar (for learning and 'computer enriched performance'), and my patch is supposed to 'answer questions' of the kind: 'If I'm on the IIm function, given the note currently ringing, which could be the next notes in a falling guide tone line? In the F ionian scale, give me the next 2 notes in a stack of thirds. Which half-diminished chords does the note D appear in?', you get the idea.
I built a simple scale visualizer with a fretboard, and for this purpose it was most useful to represent the scales as lists, like ionian: 1 0 1 0 1 1 0 1 0 1 0 1 1 By shifting bits, the other modes of ionian can be generated, same with meolodic minor etc.
Then it turned out that additional information could be represented by numbering the steps like in 1 0 2 0 3 4 0 5 0 6 0 7 1, where the numbers represent the musical values in the scale (prime, second, third etc.)
A more dense representation, but also a more technical one, would be one where we count half-tone-steps from the root like in 0 2 4 5 7 9 11 12 - this way of coding has the advantage that we could create chords/chord arpeggio in a controlled manner, with an algorithm like 'take scale, drop every second': 0 4 7 11 (a major seventh chord).
From this small example already you can see that there are trade-offs like the one between musical usefulness/human readability on the one hand and ease of applying algorithmic operations/terseness on the other, to name but one. Then there's the question of 'style' if it's more appropriate to work with look-up-tables (putting scales and arpeggios in a database like structure like a table) or with a generative approach with 'construction rules', which probably depends on the purpose. But the question of representation of chords and scales, readability vs. computeability etc still remains.
I'd appreciate any ideas, links, examples...
best regards,
Christoph
why do you want to agree upon something? it is far more interesting to fight over something, and it is far more useful to find more than one way.
you already mentioned bitshifting - that is always a nice method for such things.
another way is using symbols to express different states of a given value. i.e. instead of having the notes "60, 63, 67" here and the math expression for "inversion of input" there, you could combine the value and its state in a symbol "60 63 67 inversion" - and have an special kind of interpreter for such symbols somewhere later in the flow.
you raised already a number of good questions, and in most cases it will probably more difficult to make a decision than programming it. :)
i want to eloborate only on one little thing here, and that is the question about lookup tables vs. expressions. in my opinion calcualting things in realtime is worth the effort. the bigger a system/collection of translations is, the less work it is to calculate using math.
just a basic example of this: instead of having a table/coll full of hundreds of chords (Cmaj 60 64 67, C#maj 61 65 68,....) you could just use a dynamic list of three numbers in a [list 0 0 0], and a [+ 0] object to transpose to other keys.
in order to create different modes you would then expand this chord collection by shifting positions of the list elements using [zl rot], and so on.
-110
ok my last post was a mess, i know.
i suggest a dataflow/machine model like this:
step 1
introduce a chromatic scale consisting of 12 notes.
0 1 2 3 4 5 6 7 8 9 10 11
step 2
create a desired scale by filtering some of the notes & packing the wanted ones into a new list/collection.
0 2 4 5 7 9 11
step 3
optional: shift/scroll/rotate through this scale to create modes.
step 4
create a desired chord by filtering the scale again. the chords will be presets in the form of
1 3 5
and these presets will be ued to read from a [zl nth] containing the scale.
0 2 4 5 7 9 11
[zl nth]
[zl group 3]
0 4 7
step 5
use addition to transpose to other keys.
[+ 1]
2 6 9
step 6
use multiplication to find the base key of the desired octave
[* 5]
60
step 7
add it to your chord
[+ 60]
62 66 69
step 8
now you are ready to insert further processes such as inversion.
inversion for chords which are ranging over more than 1 octave is tricky, but i can provide the code in case you need it. :)
-110
Thanks Joe, I'll definitely check this one out!
best
Christoph
Roman, thanks for the thoughtful replies. As much as I like to invent my own solutions, over the years I came to appreciate 'condensed developer wisdom' (at least in some cases) instead of going for half-baked solutions. And I think you fully grasped my intent, it's more a strategic question right now than one of actual coding, hoping to avoid decisions that will lead to a lock-in situation further down the road. The steps you outlined are very helpful, it seems that I'm not on the wrong track with a mostly 'list based' approach.
Thanks, and best regards
Christoph
hey,
maybe it's help you to have a look at the bach project ? http://www.bachproject.net/ it's precisely aimed at calculating things with scales. It might be overkill though, and the learning curve is not trivial.
A more dense representation, but also a more technical one, would be one where we count half-tone-steps from the root like in 0 2 4 5 7 9 11 12
That's pretty much what we do. That way you can do "scales" by giving the full scale, and chordal/arpeggio information by omitting some, etc.
Thanks Vichug for hinting to the Bach project, looks very interesting, I'll keep that on the radar so to speak, as I proceed; for now, it seems to be oversized for my purpose. I must say however (on the first glance) that the ability to storce/process 'metadata' on the note/event level is extremely interesting, so I might look into this rather sooner than later.
As far as 'dense representation' is concerned, apart from the 'binary' notation and half-tone steps from the root I found another one in V.J. Manzos book 'Max/MSP/Jitter for music', and that is to store the step-widths between notes instead of notes, so the ionian scale consists of 2 2 1 2 2 2 1, MM is 2 1 2 2 2 2 1, etc. - which makes 'rotating' to other modes a piece of cake. But I'm absolutely not sure if this outweighs the disadvantage that determining the distance to the root always requires one or more additions.
bach with its "sublists" is a very good example for how to build a custom representation of musical events.
when working with my own composing systems i find myself often in the sistuation that i have to seperate key from octave. which sometimes make me think it would have been better to you use something like "{1 5}" instead of int 61. it just does notmake sense to transport numbers between processes and then split it internally into key and octave over and over again.
there are two layers. 1.) the theoretical optimum when it comes to representation (which includes the symbolic layer as well as possible metaphoric and "readablity" layers), and 2.) the optimal data form for further processing/calculation.
it is always a bit hard to make compromises, isnt it. ;)
-110
Ronan I would very much like to see your chord inversion setup..
Mine works, including for open chords but takes 10ms to output which is way too long for my purposes.
This is a big and hard problem! In addition to Bach, Common Music has a system for doing this. You can run most Common Music code in Max through Scheme for Max if you're interested in a code based approach to it. Personally, I think lisp-based solutions are the best way of representing music data, but YMMV. Julia's MozLib project for Max might also be worth checking out.
when it takes 10 seconds then something else is wrong, for exampe the decision for javascript for the task. :)
see "climbup" and "climbdown" patch.
- find min and max
- (min-max)/12 will tell you across how many octaves the incoming chord is spread
- this number is how you are going to shift keys up or down (eg 12, 24, 36...)
- for multiple inversions, just repeat/loop the whole process
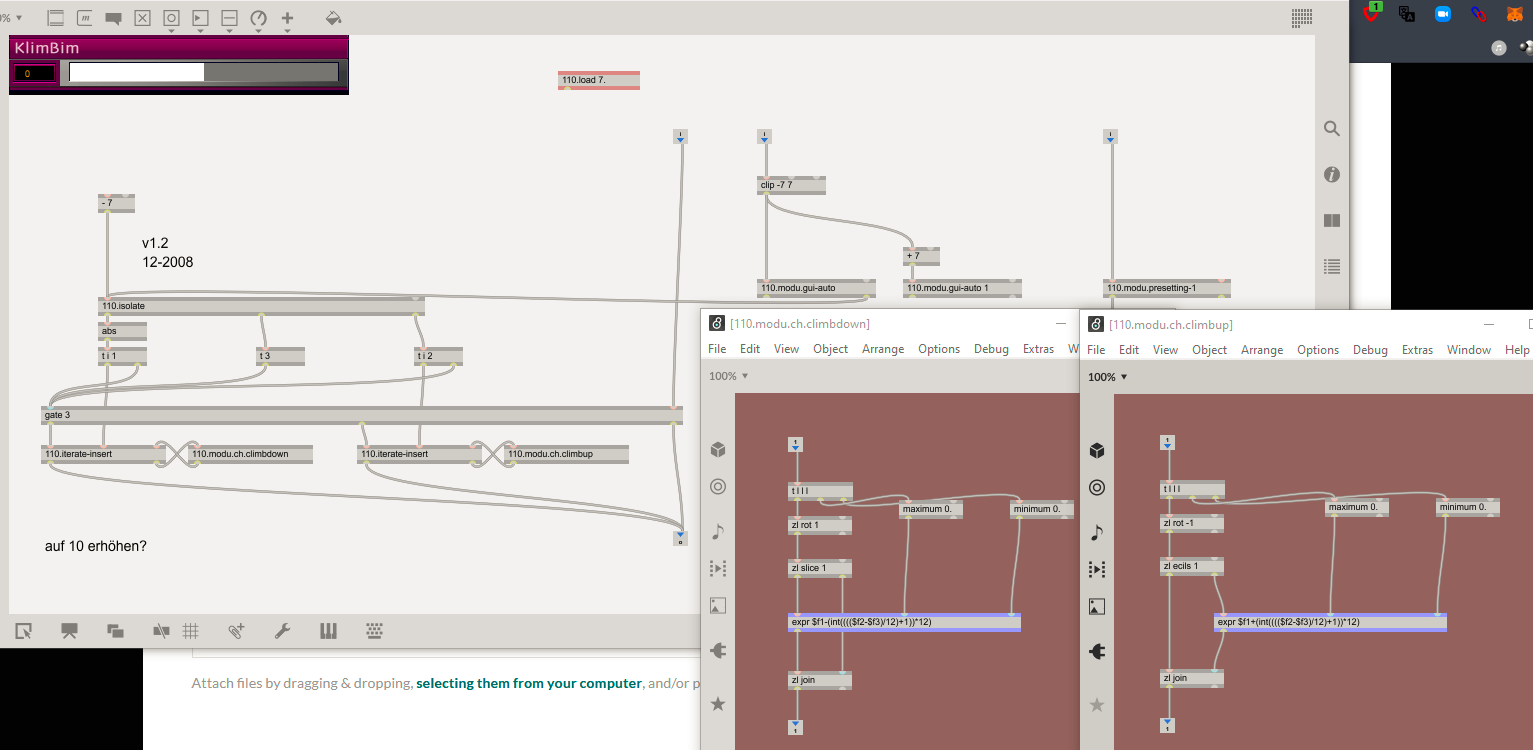
expr $f1+(int(((($f2-$f3)/12)+1))*12)
expr $f1-(int(((($f2-$f3)/12)+1))*12)
10ms not 10 seconds!
10ms could very well be the delay you get from running in the low thread (if your UI is doing other stuff). JS is unfortunately always in the low thread.
I'm not using js.
if you're not using JS and you're getting a 10ms lag, you might be accidentally going through the UI thread somehow, I'd suggest tracing that.
would a print do that? I do use funbuff for a lookup table.
Open chord C G E would invert to E C G in my scheme.
no, what would do it would be starting something from a mouse click or key stroke, triggering from a live.observer in Live, passing through a defer object, or any pass through JS. (there are other situations too, but those are the biggies)
