Crossover Filter Design Video Tutorial
Building on my previous filter design videos (see below), I use the filterdesign, filterdetail and gen~ objects to make a crossover filter that is perfect for use in multi-band EQ's, compressor/limiters or sound design applications. By using these tools to create a Linkwitz-Riley filter system, join me for a 20-minute trip into examining, testing and ultimately building a filter that doesn't otherwise exist in Max.
Download the Package used in this tutorial.
Watch other filter design videos: A Tour of Filtering Tools and Demystifying Filters.
by Timothy Place on September 13, 2016
these are a great set of tutorials tim. long may they continue. (do you take requests?!).
i implemented trond's linkwitz-riley in genexpr a while back, and use it for all my multiband processing needs.
last year we released a few additions to the oscillot package including a crossover based on it. attached is a max patch version of this module from the package, in case anyone else is interested.
nowhere near as useful as the one in your tutorial as the coefficients are calculated at signal rate (!!), but maybe someone will find it interesting to rip out the genexp code and take a look. if not should at least be compatible with beap. also paired here with graham's 2-pole crossover from the gen~ examples.
pete .
This is fabulous! Thanks for sharing @STKR!
This filter series is really awesome. I don't understand the maths, but this series explains filters in a way that focuses on the use and outcome instead of the mathematics at work.
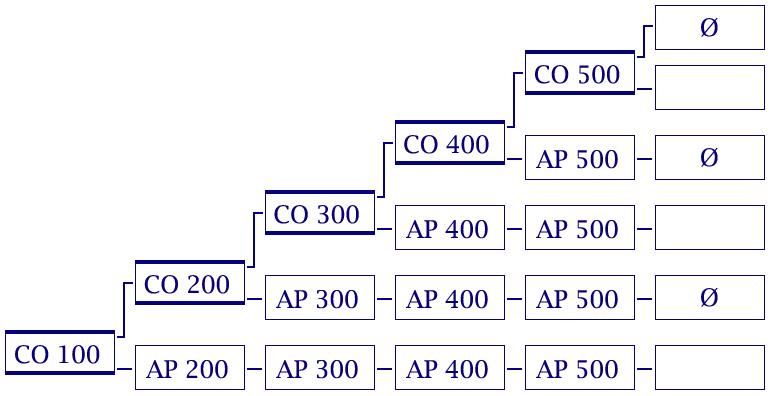
Maybe this is the discussion of a future tutorial, but how could I use the Linkwitz-Riley crossover to divide an audio stream into more than two parts (eg low-mid-high)? Intuitively, it seems like I could again divide one of the streams, like the low pass stream, and divide it again into a low and high stream, resulting in a low pass, a middle bandpass and a high pass. Will my three audio streams remain in phase? Do I need to add delay to the high pass side to compensate for the extra filters on the low-pass side?
Thanks again!
more than two bands... just chain the crossovers serial.
Nice article. Is there a way to easily implement other type of filters like Bessel (std and norm), Linkwitz-Riley, Elliptical and All-Pass. Chebyshev 1 and 2 are already included in filterdesign~ I see.
Jan
Your video has been incredibly useful for helping me with my studies! I am creating a crossover simulator at the moment and I wondered if you know of a way to implement a Bessel filter? Any information you have would be incredibly useful. Many thanks.
Laura
I haven't implemented a Bessel filter for Max. Depending on your application for the filter you could generate biquad~ coefficients using Octave's besself function ( https://octave.sourceforge.io/signal/function/besself.html ).
The same is true for an elliptical filter.
If you want to have a filter than can be dynamically modified (as the filters in filterdesign are) then it will take some significant math chops. A good starting place (apart from the Octave besself code) is this: https://vibrationdata.wordpress.com/2012/11/11/bessel-lowpass-filter/
Hope this helps!
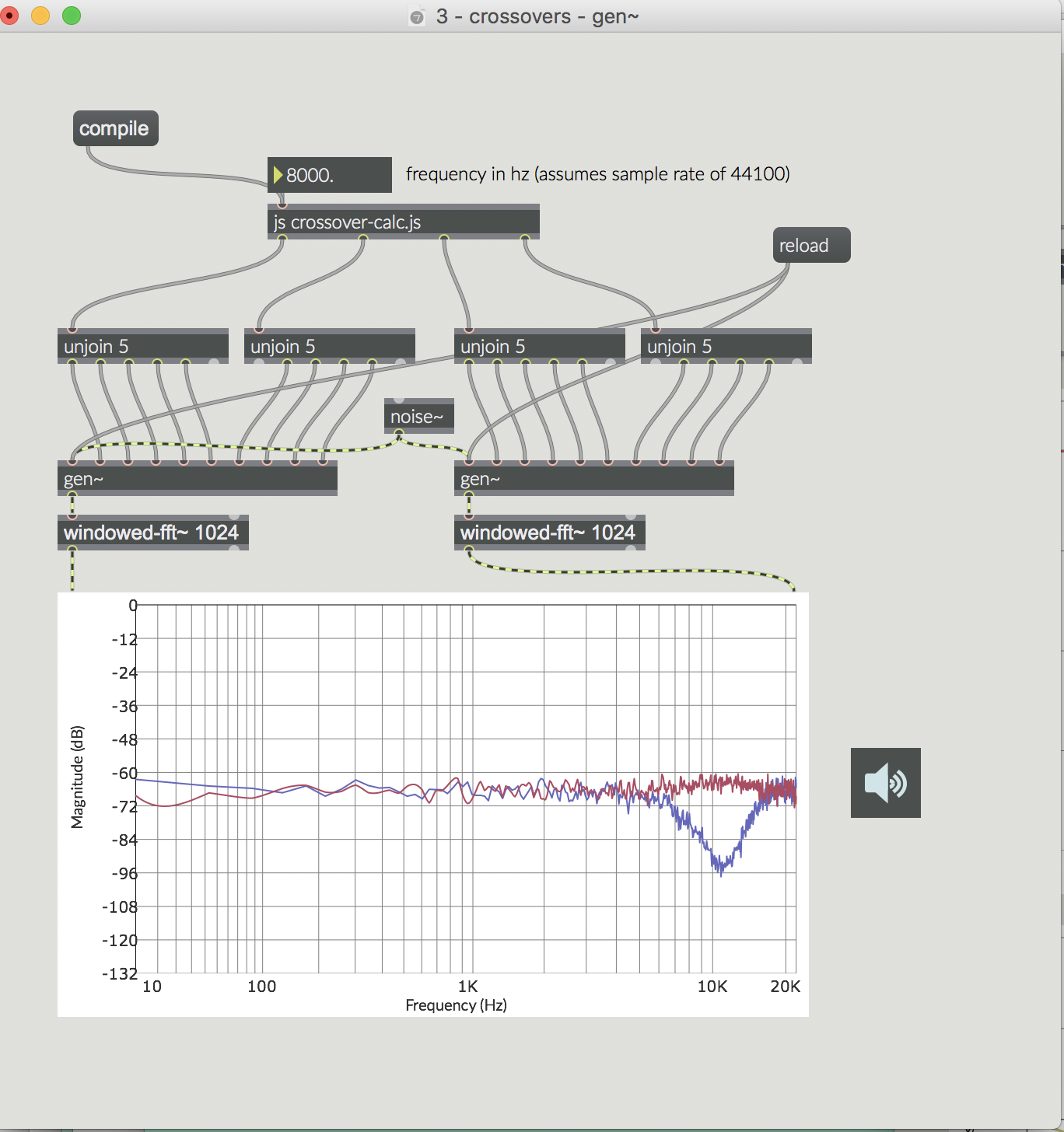
Thank you Tim for this very insightful and helpful tutorial. I tried to run the "3 - crossovers - gen~" tutorial patch for the Linkwitz-Riley crossover but I am getting the wrong frequency response as you see from the attached screenshot. The java script seems to be OK as I get the correct response in the "2 - crossovers - lr" tutorial patch using the filterdetail object. I am running as required at 44100 Hz and have changed the I/O and signal vector sizes to various values in Audio Status but nothing changes and the problem remains. I am puzzled at what could be causing this. Any insight would be appreciated. (Max 7.3.5, Mac OS 10.12.6).
i am posting this question here because it is releated to a similar context:
how far away is a "regular" biquad from a butterworth (read: cascades of 2) when it comes to its main property, the absolute frequency flatness at the crossover point / rated frequency?
I updated Max 7.3.5 to 7.3.6 and the problem I reported above went away. The spectral plot now shows the same curves as in the tutorial. Does anyone have a clue why?
I found out that the issue with the wrong curves in the spectral plot~ I reported earlier has nothing to do with the version number of Max but rather the signal vector size. For the spectral plot in that tutorial patch to display the correct curves the signal vector size must be 256 or smaller.
However I now realized that there is another issue, this time with the sound coming out of the gen~ objects in that tutorial (the one about Linkwitz-Riley gen~ based filters). It is best heard with pink noise (but it is detectable with any wideband audio) as the input (as shown in the attached patch). Basically, as you change the XO frequency either continously (e.g. with a flonum object or live.dial) or by entering discrete values, you will hear a thumping noise/click at every change. This thumping noise is most evident for XO frequency values below 400 Hz and gets very loud at the monitors/speakers (when set to regular listening level) when the XO frequency is lowered below 100 Hz. It is also clear from the audio in the attached patch tab the thumping noise is only on the HF band of the 2-band crossover.
I was able to stop it when the XO frequency is changed by discrete values by setting a gate~ that stops the output of ten~ from going out to ezdac~ for about 15 ms, but that trick does not work well when the XO frequency is changed continuously.
Tim, do you know what is causing this noise? Is there any way to avoid it?
Thanks in advance.
using sqared topology is less accurate than using 2*butter.
Lots here to respond too, but first, the Butterworth is not something to be compared to a biquad. In fact, the typical implementation of a Butterworth filter is performed with 1 or more biquads. You can use the [biquad~] object or the [cascade~] object.
Regarding the spectral plots, yes, the [windowed-fft~] abstraction has some requirements of the vector size. Specifically, your signal vector size must be 1/4 the size of the FFT or smaller. This is documented in the "spectral" tab for the [plot~] object. I am hoping to eventually replace this abstraction with an external object that will remove these undesirable sensitivities.
Regarding the "thumping" or other discontinuities when the frequency of the filters change, this is a known problem with filters, particularly when there is feedback in the filter. Do you clear the history when you change the frequency and induce a pop? Or leave now-wrong data in the history?
The [biquad~] object has an attribute called "Smooth Coefficients" which implements an approach to helping with this problem. It looks like the [cascade~] object does not, which is unfortunate. I'll make a note to research this further to see if we can add it.
Cheers!
Thank you Tim for the reply.
I am not sure I understand what you mean by "clearing the history". There is not much documentation on the history object in gen. Could you please clarify how to clear the history. Perhaps in the context of the tutorial "3- Crossover - gen~" that you posted originally. Would clearing the history solve the thumping issue?
Hi,
"Clearing the history" means setting all variables used for feedback to zero. It will trade the thumping for a popping sound which you probably also don't want. So... yeah... also not ideal...
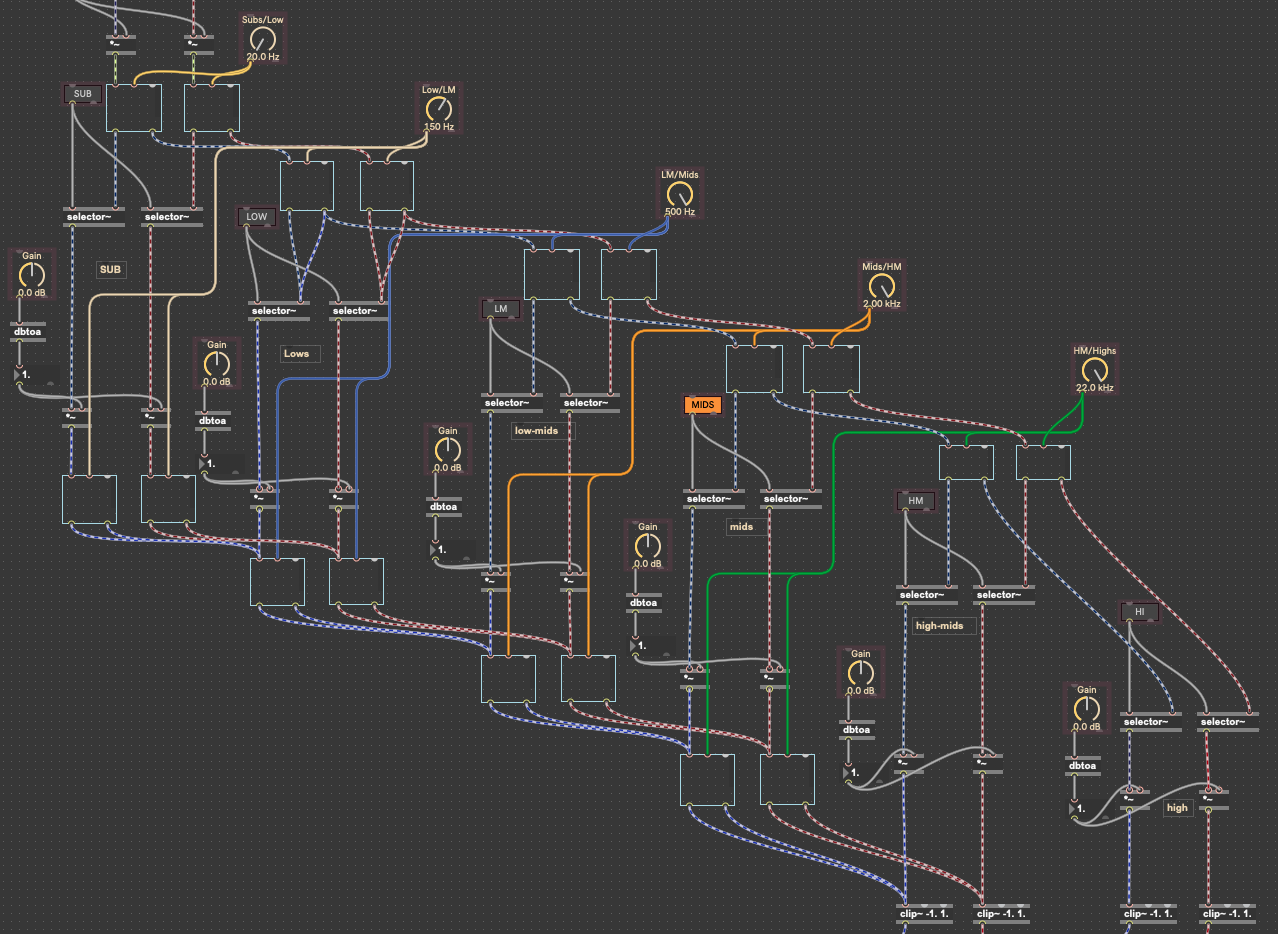
Thanks Timothy! This really helped me make a multiband compressor in gen and learn a great deal about filterdesign. I ported your JS crossover calc into the new event driven [gen] if anyone would like it. it also dynamically adjusts to your samplerate using dspstatus.
the 'samplerate' and 'SAMPLERATE' constants don't seem to function correctly in event driven [gen] on my system samplerate = '200.' when set to 44100.
Thanks for this report @lysdexic. I can reproduce and have ticketed for further research.
I had initially thought that perhaps my scheduler was running at a 5ms interval and so 200 was a sensible response. But I see that my scheduler preference setting is 2ms, so I'm not sure where the 200 is coming from.
Hey Timothy,
This whole lesson has been really informative and I really appreciate it. One of the questions I still have (and haven't been able to actually find an answer) is no matter what form of LR-4 I've tried, the final gain is always increased. I've seen one plugin that uses a non linear phase LR-4 filter that doesn't have any change in output gain, but I haven't been able to actually recreate it in max.
Turning the gain down to compensate for the change also doesn't seem to be the solution because at that point it's not actually preserving the original signal. What is this gain change from and how is it avoidable?
Thanks.
Hi Tim, I wanted to extend what you did here to an 8th order Linkwitz-Riley, however the code library from which you took the code for the js crossover-calc.js object in your example has only 2nd and 4th order L-R filters. Any advice on how I can extend to 8th order?
Thanks
Adam
higher order by serial cascading.
To make a proper 8th order LR, you must cascade two, 4th order butterworth filters but make sure that the orders have correct Q values when stacked!
https://csserver.evansville.edu/~richardson/courses/EE410_Analog_Circuit_Synthesis/resources/handouts/ButterQValues.pdf
Yo peoples... I made a pretty cool Multiband compressor but no matter how I stack 4 of these filters (to get 5 bands) I get different frequency responses, none of them linear. Im basically going from the highpass of the first pair into the next pair etc which has given me the most even response but its still not flat. I'm assuming this is normal operation as the filters phase response stack up and create these discontinuities in response. Do I need to go searching for another filter coefficient calculator to get a linear response 5 band crossover?
No, you need to understand the theory behind multiband crossover filters.
To that end, check out this link:
https://www.modernmetalproduction.com/linkwitz-riley-crossovers-digital-multiband-processing/
There is also an interesting conversation about it on the JUCE forum:
https://forum.juce.com/t/perfect-crossover-filters/36125/9
Basically it boils down to introducing an extra Allpass filter stage every time you introduce an extra band.
That will keep the phases of the different branches coherent, so you'll get perfect reconstruction when you sum the bands together.
There are also a few papers around that describe this technique in more detail and from a more technical point of view. Google is your friend.
hey all, cool topic, thanks for your interesting successive inputs !
i need a 3 band crossover ; so using two crossover linkwitz-riley should work, right ? and following @Luigi's link, it seems introducing an allpass filter at the output of the lowest band plus inverting the mid range band phases (am i correct in assuming this just means pluging a [~* -1] for that band?) should do the trick, but how to get the allpass filter to the desired frequency (which seems to be the high cut frequency) ? From max's documentation, we can see the phase change, but there is no direct correlation to a specific frequency. I'm guessing the frequency in question should have its phase changed by 1 pi ; but how to calculate that from giving allpass only delay and gain parameters ?
Also how to interpret the differential equation "y(n) = -g x(n) + x(n)-(DR/1000) + g y(n)-(DR/1000)" : is it simply "y(n) = -g*x(n) + x(n - delay) + g*y(n - delay)" if you assume the delay time in samples ?
edit : apparently for 3 bands, if i don't put an allpass and don't touch the phase, using 2 chained Linkwitz ; it's relatively okay if the low and high cutoff frequencies are sufficiently far apart (at least graphically...)
when you only have an example available how to use the allpasses for 2 and 3 bands, it is a bit tricky to construct the same thing for 5 bands.
"but how to get the allpass filter to the desired frequency (which seems to be the high cut frequency)"
i think this rule is correct:
if you have n bands, A, B, C, ..., A must be donated n-2 allpasses at the same frequencies (and order) of all crossovers except its own (A vs B) (the order of insertion theoretically does not matter)
the more bands you have, you might even be able to save a few filters, some guy built a 10-band design with 40% allpasses saved in flowstone.
unfortunately until now i was not able to rebuild in max.
you mean he replaced some band filters with allpasses or something ?..
but anyway, no idea how to infer allpass's "center frequency" from its gain and delay parameters ?
not replace, you insert it in addition to the crossovers to correct that little bit which is missing to make the sum of A, B and C the original again.
it doesnt do anything but correcting the phase shift the crossover at the other band(s) is applying, too.
an allpass is basically the same as the crossover on the other signal, just with the outputs of hf and lf summed.

Thanks @luigi that makes perfect sense. Pretty sure each time you run a highpassed signal into a lowpassed signal its getting flipped anyway... ? So you only need the allpass filters in this instance. which @vichug you would use the phaseshift~ object, which is a second order all pass and has a parameter for centre frequency.
The next objective is to get all the Q values correct, as im still getting some very small dips.
I have incredibly close to a flat frequency response with this setup. The crossovers are set to 160hz, 800hz, 4000hz and 11000hz. Q values of 0.7071.
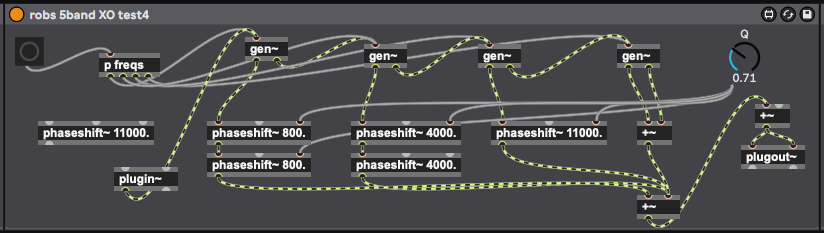
arent you supposed to built the allpass from the same butterworths?
So, the order of the filters might be off. If you have LP and HP filters at the 2Nth order, you need an AP filter at the Nth order to compensate for their phase response. A very common configuration would be to use 4th order Linkwitz-Riley filters (24db/octave) for the LP and HP and a 2nd order AP for the phase compensation stage.
so phaseshift~ is 2d order allpass filter ? and two phaseshift~ in series would be a 4th order allpass ?
Correct @Vichug
Although building an allpass from the LR filters, like Roman said, does make sense. I'm yet to try it though, in any case phaseshift~ should be much less demanding, cpu wise.
Yes, what Roman said is absolutely correct. You could also build it from the Linkwitz-Riley filters. Actually it would be LESS demanding cpu wise than a [phaseshift~] solution because you could theoretically use the same Linkwitz-Riley lowpass and highpass outputs (at Nth/2 order), so you don't need to recompute a new filter. So you would start with a lowpass 2nd order Butterworth and a highpass 2nd order Butterworth with the same cutoff frequency. From these two filters you create the 2nd order allpass. Then you cascade these two 2nd order Butterworth filters into another set of lowpass and highpass 2nd order Butterworth filters to create your 4th order Linkwitz-Riley filter (that is exactly why a Linkwitz-Riley filter is also called Butterworth squared). Now you have your 2nd order AP, a 4th order LP and a 4th order HP for the price of a 4th order lowpass and highpass. The allpass comes basically for free. Pretty cool, eh?
(i dont understand how you could use the same filters twice? but) in 64 bit max (i dont use gen) you should be fine to calculate the filter coefficients for your biquad-butterworth already squared, then you only need 2 instead of 4 biquad objects.
i also remember reading about some trick where you would use 6 or 18 db filters (instead of 12 or 36) for the crossovers, which allows some interesting designs regarding this allpass story, too.
sry if that is going offtopic: any idea how we can add (serial) filters in a filtergraph display?
visual proof methods are so much more error-free than sonic ones. :)
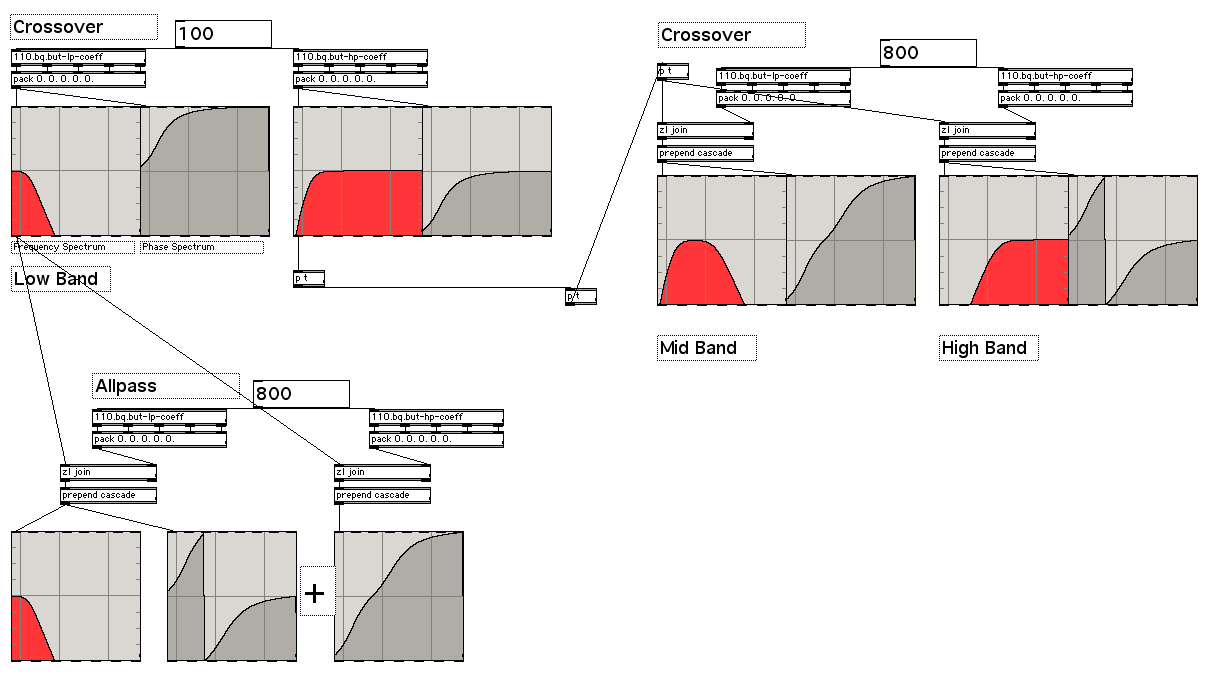
i think you can do that with filterdetail and plot~, by adding filter's FIR, but with filtergaph i don't know...
Amazing reboot of this thread, loving it
Would phase shifting vectors with [phaseshift~] in and out of gen~ affect things in strange ways? Would it be best to avoid strangeness to keep everything in [gen~] land or is phase shifting sample vectors negligible in this DSP chain?
to me it makes the most sense to use exactly the same filter code for the allpass, first of all because you never know what an external is doing.
but i have often enough made such assumptions and then it turned out that i was wrong. :D . so, no statement.
yea, with filterdetail it could work, let´s see if i find a way how to average the phase amplitude values of its output.
the picture i posted is nonsense anyway, that´s only 6db instead of 12.
Hi,
Sorry to ask this question:
Given the case that you can convert a LP filter to a HP by substracting LP signal from original signal, resulting by definition in a perfect flat filter response after summing and a CPU usage close to 0, i am wondering what are the main reasons why this design is never in use in multiband configuration ?
(For the moment, it is the only way i have found to find back my original signal by summing the bands created by this way.)
you can do this... for 2-band.
as soon as you have 3 or more, the idea behind it stops working; do the math ;)
I've got 5 bands working perfectly now using the LR coefficients (no phaseshift~ like I was doing before). Basically the first band needs an allpass (a lowpass and high pass in parallel) using the coefficients from the second band split, this continues until you reach the last 2 bands which do not need allpass filters. This results in a linear frequency response, but is 180 degrees out at the crossover point with 4th order filters. So if you run this in parallel, you get cancellation at the cutoff points... perhaps with 2nd order filters it could be in phase everywhere? (My initial goal was parallel multi-band compression).
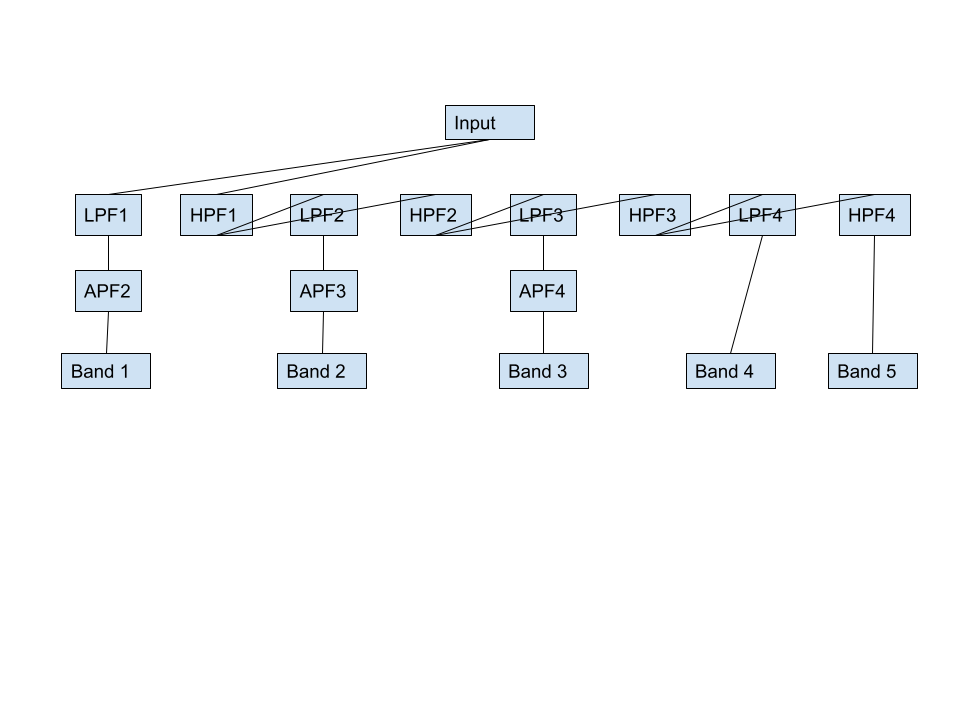
(i think) you are supposed to add ALL the "missing" allpasses into the "new" bands, not only one.
so the third band get one allpass, the fourth band gets 2 and the fifth band gets 3.
and you forgot to phase invert every other output. :)
Ah yeah... that makes more sense with the phase flips, thats a lot of filters though.
So thats ”linear-phase” and wont result in any cancellation when ran in parallel?
if you have a really good picture of what happens, then for 8 or more bands you might find ways of optimisation and save some filter modules, but then the whole layout becomes a mess because you also have to change the order of how the the splitters have to be connected
a naive explanation of the basic idea (so that i understand myself better :) ):
- every splitter "does something to the phase" of its two outputs.
- this "something" will be present in everything what follows
- and so it has to be "compensated for" (by doing the same) in everything else "prior" or "parallel" to later processes.
that strategy should be correct for that hardware-like crossover design consisting of 4*3db butterworth cascades.
it should also work for IIRs of other topologies and for fft filters (but then why bother) and for combs.
it might work for 12*3db, too - but i never got it to work.
...
now... there is one problem left.
this design was once made for speaker systems. or on in other words: for situations, where you later only sum the frequency bands again. (after transduction in the case of a speaker system, but well, it is still "summing".)
but your multiband compressor (and most other usual suspects for frequency selective processing) "is an eq".
i.e. you are going to change the amplitude before summing.(!!)
...
*insert deep breath here*
...
*drop random keywords such as hilbert transform and symetrical filters here*
Did my best to follow along and reached this point, where the split patchers are pretty much OP's code (left out being Lows, right out being Highs):
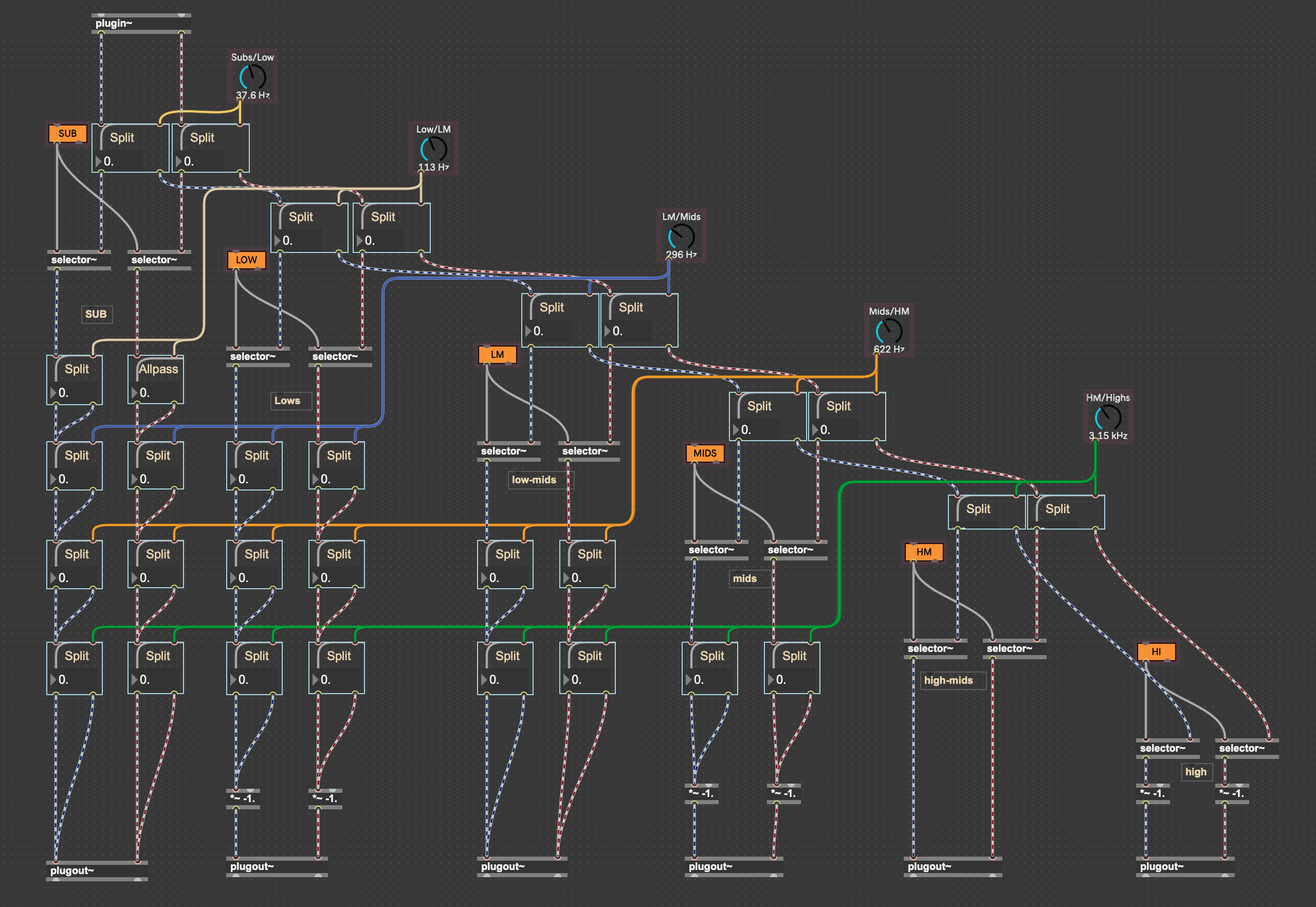
But I actually do get cancellation points at the exact split frequencies, when adding the Allpass and phase flip, probably I'm doing something wrong here, anyone has a clue ? (example below on pink noise)

I've corrected my device as I got the phase inversion wrong, here is the new structure:
No phasing any more, it seems fine, I think have a signal inversion though, I've added a *~ -1. to both inputs to correct that (not showed in the picture below) even though I don't know where it comes from (a 360° phase diff between LP and HP should not lead to that).
Still I don't get a sample accurate response when I sum back all the components (i.e. when all bands are active, I should get the exact incoming signal, but that doesn't happen). Soundwise I can hear a slight difference especially on low content (the rumble seem a bit lower through the device on a bass note). Could this be related to the filters group delays caused by the filter chains (i.e. should I add sample delays to some of the outputs and declare that as a latency, as each filter adds like 1 sample delay) ? Normally the phase delays have already been compensated by the AP filters, but the group delay probably not ?
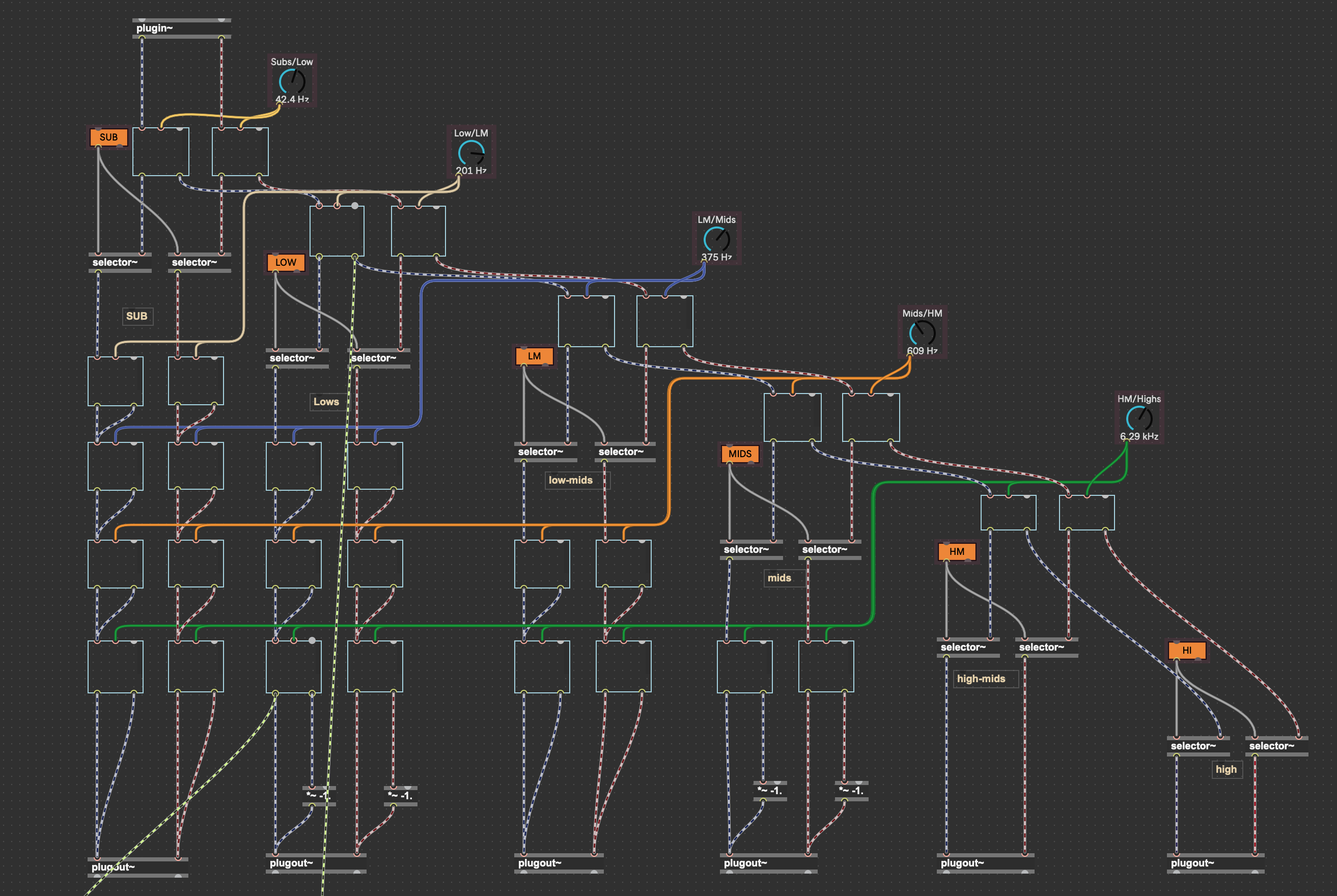
i dont understand that new position for the øs, could you add the new frequency plot?
group delay should not be an issue with a bw - and afaik impossible to compensate for. (upsampling the filters will lead to new group delay when downsampling again)
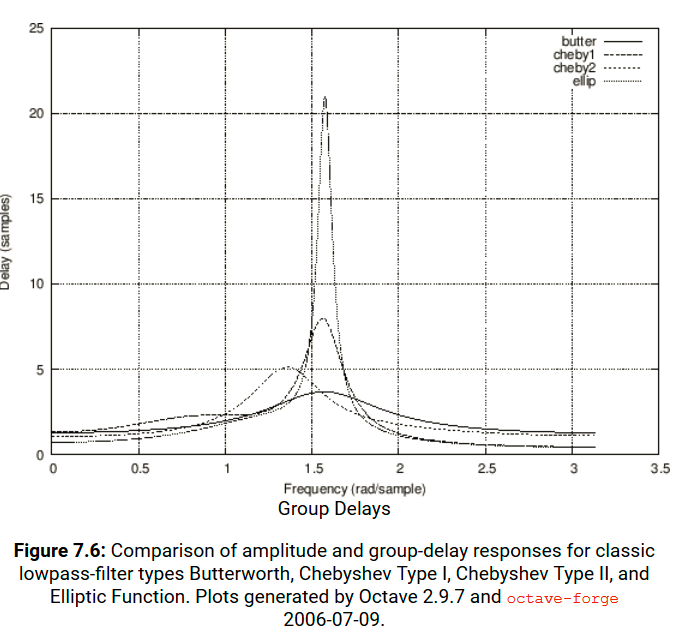
It's pretty much identical to the input signal, so there is no change in the spectrum, but yet the signal is slightly different :/


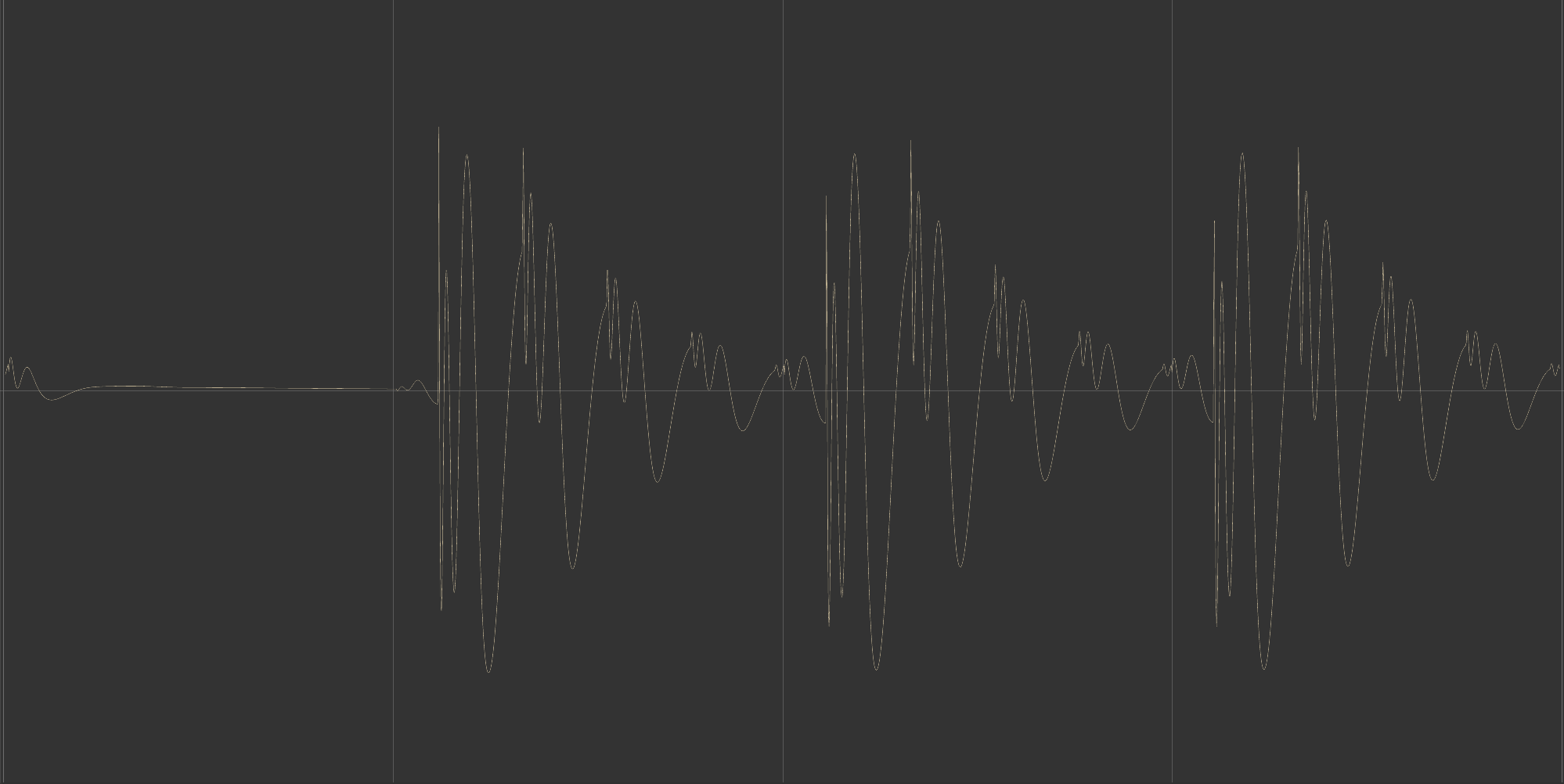
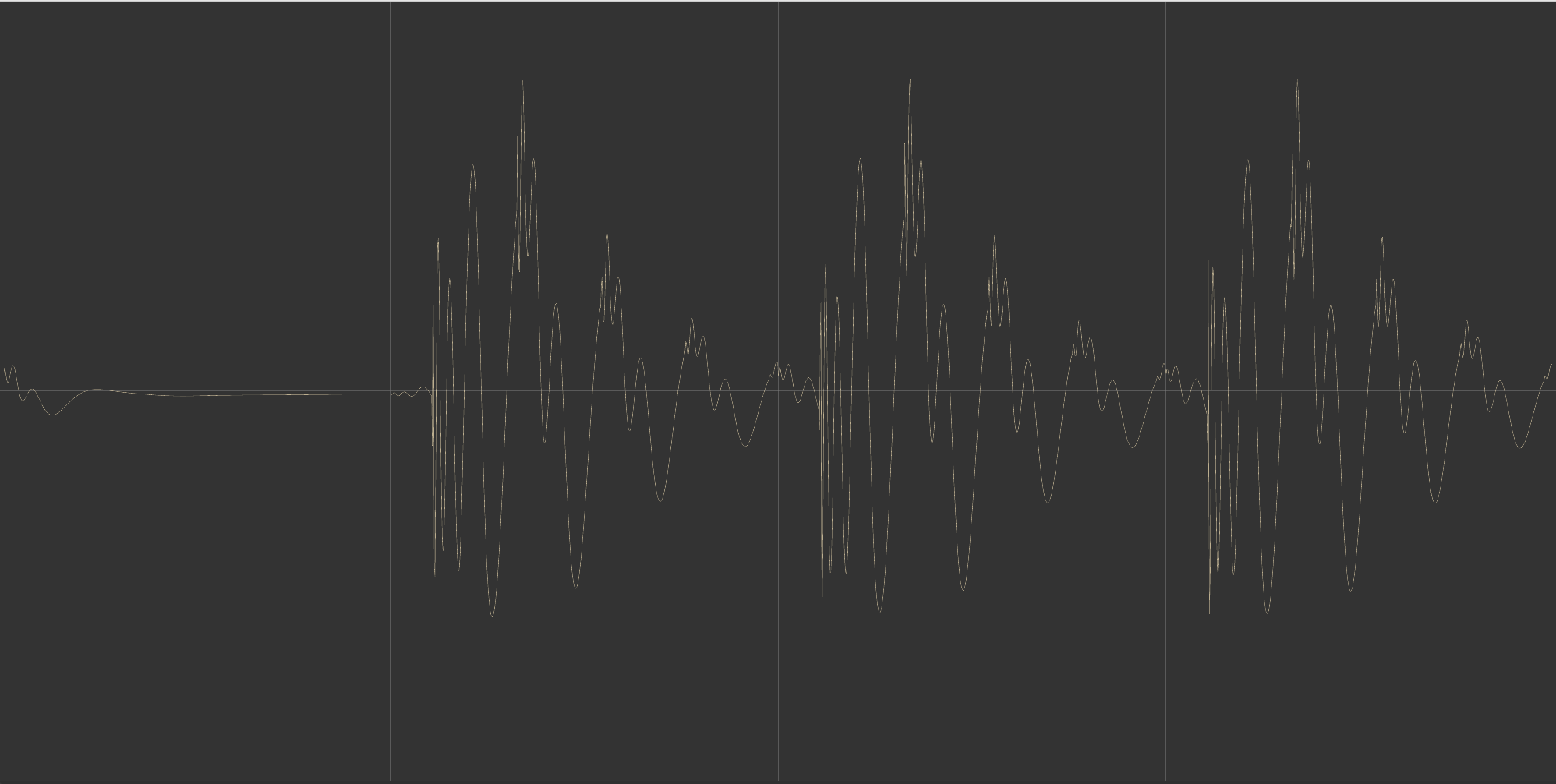
As you can see, the difference is not huge but it's there.
Can't explain the signal inversion either. Tried to use Oscillot filter instead of mine, no change...
Oh, BTW forgot to mention I'm not using BW filters but Linkwitz-Riley to avoid the phase delay, that's why I was talking about the group delay only.
an LR is usually made of 2 butterworths. (or actually 4) (you´re using an external?)
okay, but it looks much better that the first one^^ how did you get the phase right now, can you explain?
can one say that this means that the inversion in the original linkwitz diagram has to be included into the compensation allpass? the more i think about it the more it makes sense...
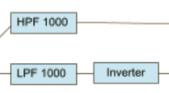
==
to compensate for runtime delays one would eventually have to truncate the possible filter frequency settings so that it always ends up with runtime delays of integer sample count. i have no idea how to calculate it though.
and btw. a flat sum (frequency) doesnt have to be of the same phase than the input. it is only an allpassed version of the input, after all.
i wonder what happens when you compare signals which are a form of frequency analysis of in and out? (like a bandpass->average kind of thing.)
Here I used the xover shared a while ago by STKR, with its default params, it's a second order Linkwitz-Riley, I chose this one as it's relying on gen~ and not JS for the coeffs computation, it seems CPU heavy, but it allows for smooth filter freqs changes without incurring any audio artefacts. That's important for me as I'm aiming to automate these frequencies without any phase issues or audio glitches.
I probably should send that part of the gen~ outside the bpatchers as it's highly inefficient (the coeffs are computed in each gen~ so some of them are done up to 10 times), but I'm no expert in gen~ so I'll leave that for later.
WRT the phase, I removed the LP [*~ -1.] and only kept the one of the HP, wouldn't be able to explain why, but it seemed to me that somehow the LP output and the HP output were opposite phases at the crossover freq and that would explain the cancelling right there (though Tim showed that they should be 360°, or maybe I got it wrong and that would be true for 4 poles not 2 poles).
Somehow empirical admitedly but it's so close to a sample accurate crossover that this is the reason why I was thinking about the group delay added by each step of filtering cause a few samples error in the end.
Auto correcting myself, in my device I made (at least) two mistakes uness someone explains me otherwise:
- first is that I'm using 4th order Butterworth in my subpatchers so the total phase shift is 360° both for LP and HP, thus no need for the phase inversion,.
- second I've put way too many AP filters, each stage can be instead fed into next one as they are in phase, huge CPU saving.
Of course the resulting phase shift is 360*5 = 1800°, so nothing like a zero phase impact but frequency and phase wise everything seems to be synced.
Reversing that phase shift, from what it stands would necessitate applying the same allpasses to the time reversed signal, which of course is undoable in realtime. Then, substracting the (again) reversed signal to my original input where all gains are at 0 should lead to a null signal (apart from approximations in calculus). Please correct me if I'm wrong ?
while i dont understand why mine does not work correctly, your approach seems to be even more weird.
"first is that I'm using 4th order Butterworth in my subpatchers so the total phase shift is 360° both for LP and HP, thus no need for the phase inversion"
this is only true if the frequencies of all bands are the same. ;)
the phase shift amount of HP and LP is always the same for the same order, the problem is more about the phase shift between the stopband the passband in every filter.
Sorry if I sound totally dumb, but I don't understand this sentence:
"the phase shift amount of HP and LP is always the same for the same order, the problem is more about the phase shift between the stopband the passband in every filter."
The filtergraph of the 4th order butterworth for LP and HP show their phase shift are identical (from 0 to -360° throughout the frequency spectrum) so shouldn't they be totally applying the same phase distorsion (hence being in phase with the other) ?
Not meaning that they don't cause distorsion of course, just thinking that it seems to be the sameat any given freq, removing the need for phase inversion of any of them.
unfortunately i am on the same elementary school level like you when it comes to understanding and planning phase correction filters for EQs and stuff, it is all trial and error here, too.
the main issue is nothing new: the word "phase" has about 17 different meanings in audio DSP, so if you have not studied it, you never really know which "phase" you read about in a source text.
let me sum up again what i think i know.
1.)
the phase spectrum of a butterworth looks like that:
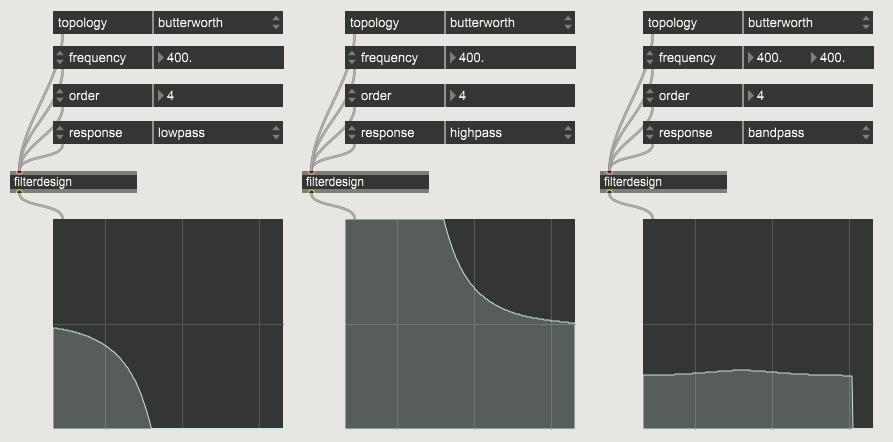
(maybe it is not always the best idea to trust cycling74 externals, but if we do for the moment...) as you can see, splitting up an input signal using a linkwitz-riley 2-way frequency splitter and summing the low and high again, leaves a small mark in the phase spectrum, which is now no longer exactly linear (i.e. different from the input signal.)
2.)
a distorted phase spectrum alone is completely irrelevant when applied to a music signal - you wont hear anything interesting or annoying. this lead s us to...
3.)
...but it is getting relevant as soon as you mix two copies of the same signal (or parts of it) with different phase spectra together again, which is what we do, as soon as we use 3 or more frequency bands in a spaker or in an EQ.
that is why mr. linkwitz himself came up with that graph for his speaker design:

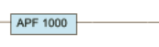
the idea is a simple as f*ck; an allpass filter doesnt do anything to the frequency spectrum, but has the same phase spectrum as a bandpass - or a parallel combination of highpass and lowpass i.e. a crossover.)
so we insert one allpass of type "donald duck" as correction filter into all frequency bands which did not pass the "donald duck" crossover themselves, and now all parallel signals have the same distorted phase spectrum, and hopefully the artefacts are gone.
4.)
you must very careful with the order of butterworths. some digital "butterworths" are 3 db, others are quadratic and have 6 db like all other topologies have as only option. the original analog design by linkwitz uses "4*3db", this corresponds to only "second order".
i am not sure if you use a proper test setup?
- white noise in
- dont change the amplitudes of the bands, but
- move the frequency settings around.
as soon as you hear an effect of that quite clear, something is still wrong. :P
All this is easy peasy with 2nd order butterworth filters rather than 4th order. I’ve made a 5 band linear phase cross over only calculating lowpass coefficients and used the phase flip trick to turn it into a highpass where necessary. Sounds much better to my ears with the gentler slope as well. Less phase shift to have to correct for in the first place. Im going to remove the LR stuff from my patch.
OK Roman, yeah there is definitely a change in the sound when sweeping frequencies, I can't hear it on white noise so it's probably quite subtle, but it's clear on a sawtooth input, some freq are slightly boosted when sweeping.
Robert, my initial issue with the BW filters is that they don't seem steep enough for a crossover so I tried the LR instead. Some designs now provide multiband processes with crossovers up to 96dB of steepness which seems a hell in terms of phase distorsion, I wonder how they achieve that !
Probably need to study more, but the exercise is yet interesting, though I'm only touching the surface of the complexity of filters I'd say ;-)
I'm using lysdexic's crossover https://cycling74.com/tutorials/crossover-filter-design-video-tutorial#reply-5e4377db8a6f416613deaf7c but the lowpass won't pass audio if it's initialized around 100 Hz. Seems I need to initialize it around 8000 Hz first and then set it to 100 Hz.
>>Probably need to study more, but the exercise is yet interesting
it could be a good idea to finally give up on the idea to find the best-as-possible way and use phaselinear "versions" of the very same filters instead. (and then deal with the latency that causes...)
with FIR it is quite possible to do what you want, but it is a mess to implement the recalculations properly when you want to have a user controllable frequency parameter.
I was thinking I was going to necro-bump this thread, but it looks like it's been popping off recently!
So there's quite a bit above I don't understand, so I'll start with a question.
I've been doing this thing where I have 7 cascaded cross~ filters which are being driven by melband analysis elsewhere as a way of applying a per-grain EQ matching of sorts. Now, using cross~ filters this way isn't ideal, but the overall effect applied is still good, so I've been going with it.
Basically this:
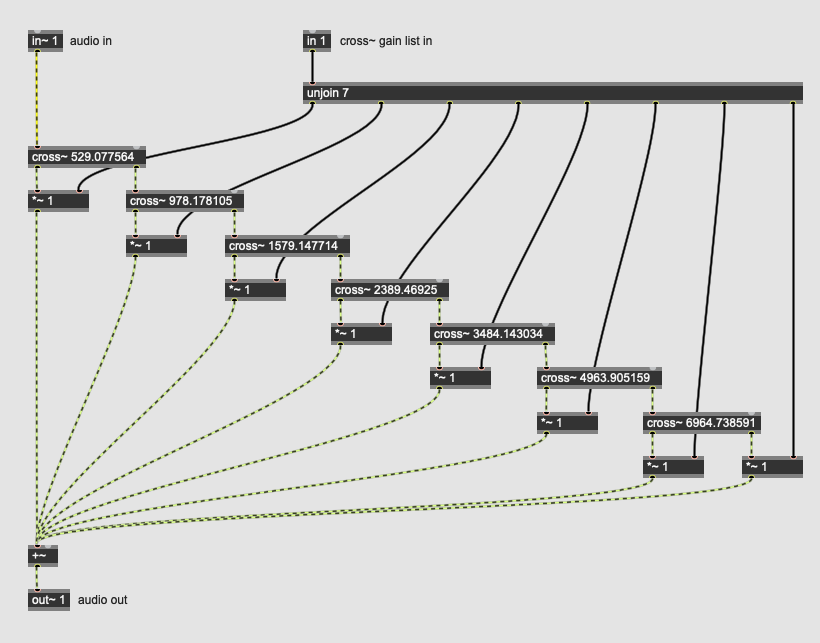
Thankfully in my case, the frequencies are constant, so I don't need to recompute things unless the SR changes.
So if I wanted to recreate this set of filters using the LR gen~ version(s) above:
-would I also need to include allpass filters in a bunch of places too?
-would it be (substantially) more computationally expensive? (vs cross~ sans allpasses)
-is there a better way to get to similar filter contours? (my actual code uses 40 melbands, but after applying frequency compensation I "downsample" it to 8 bands to save on cpu)
a common approach these days is to use trapezoidal svf filters as its much more efficient to get all the various filter types (would only work for 2nd order - stacking two first order filters or 4th order - stacking two 2nd order filters) and it can all by modulated in realtime if necessary... any more than 2 bands you will need the allpass filters to compensate for the phase shift of proceeding bands. I've stayed away from LR due to the fact that if you want to run it in parallel then the dry signal also needs to be phase shifted which doesn't really equate to a dry/wet, more a 'wet and partially wet' due to the added phase shift required to avoid notches when used in parallel. My approach has instead been the 'salami slice' approach which has bumps in the highpassed signal but can be used in parallel without any allpass filters. this approach is basically using 2nd order lowpass filters only and then subtracting the input from the lowpasses to create the highpass, you can cascade filters in this way to create as many bands as you like and the sum is perfectly flat, but if the gain is changed then there is a small bump which can be mitigated with low Q values. On my to do list is to implement this method of filters to get 'actual' linear phase IIR filters and then use the same 'salami slice' method which wont have the bumps in the highpass because they dont have any phase shift, as they are effectively FIR filters just more efficient and lower latency... https://vicanek.de/articles/ReverseIIR.pdf
it seems that good crossovers are not a trivial task. Linkwitz riley is more of a thing from speaker design rather than modern music production. I think there might be some research papers from AALTO that may be of use to some.
yes, using the cross object requires allpasses for 3 or more bands.
but all of our testing patch design approaches above have the same issue: as soon as you change the gain of the bands, the flat phase response property is gone.
it is to be expected when you think about it, but somehow impossible to grasp during creative work.
to make any existing filter symetric... you can setup a windowing system which runs a parallel copy of the input signal backwards through an identical copy of the filter and then sum the results - with the right delay.
note that it is one sample less than the window lenght (see FIR... symetric means odd number because there is only one n^0.)
for some extra fun you´ll also have to delay any modulation of the frequency parameter for the reversed stream.
in MSP it is half a monitor of externals and an absurd CPU hog.
Could someone please help me modify this gen~ code to have 5 bands? I'm having a bit of trouble getting it working properly.
move js in same folder as patchers