Creating a guitar overdrive pedal (by using frequency domain?)
Hi guys,
I’m a Max MSP beginner and I have been working on a project for a few days, but I just can't get ahead.
I would like to recreate a guitar overdrive/distortion pedal (yes I know, another one sorry...) and I have already read some threads about it in this forum, but unfortunately they could not help me.
My Max patch idea:
Audio input —> transfer to frequency domain (maybe fft~/pfft~ ?) —> receive Values of existing frequencies (f) —> add f * 2 and/or f * 3 and/or f*4 and so on…
I’m pretty sure I’m gonna need something like buffer~ or lookup~ resulting in some latency, but I’m ok with that for now. Do you think this kind of signal flow is possible?
I also read the „Dynamics Tutorial 3: Distortion“ Tutorial but I didn’t really get that. The Guitar Processor Tutorial was also a good starting point but I’d like to prevent using overdrive.
I also tried the tanh~/atan~/clip~ objects (ideas from this forum). They’re working but I’d like to understand or even recreate what it is really doing.
All the best,
H.S.
tanh or clip literally (i.e. mathematically) "distort" the input range.
say you have music stream, then in it there are sample values between - 1 and 1.
if you now apply [clip~ -0.5 0.5] to it, incoming values of 0.4 will remain 0.4, but 0.6 will be mapped to 0.5
the former linear range of 1. - 1. is transformed to a curve - until it totally clips at 1.0
tanh~ is only used because it is cheap and simple and very similar to how analog components treat signals when you overdrive them.
you can use it on a normal range, or biuld something more sophisticated in the range of -pi - pi and process only signals above 0db/a.
to check or "understand" what they do, take a scope~ object and monitor how steady signals are changed from such processes.
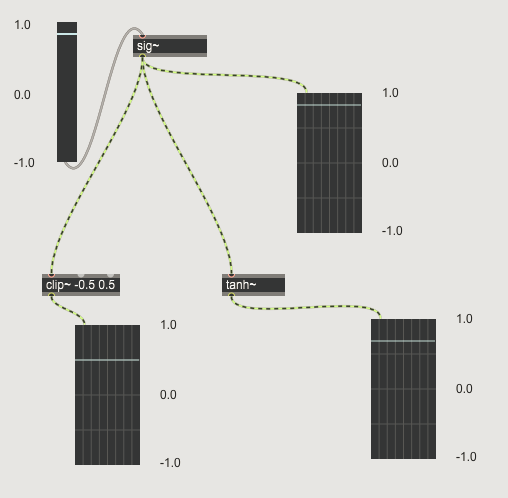
It took me a while, but I rebuilt your patch and now I understand clip, tanh and atan and their differences, thanks! Clip limits the amplitude to the given value, tanh is more flexible (comparable to softclip?). Atan gave the same result as tanh.
"tanh~ is only used because it is cheap and simple and very similar to how analog components treat signals when you overdrive them" So I'll probably work with that, thanks!
"you can use it on a normal range, or biuld something more sophisticated in the range of -pi - pi and process only signals above 0db/a." I didn't quite understand that. What would be the advantage of choosing pi as range limit?
Now I know how I should work further, but I would like to try the fft variant, at least theoretically.
Is it possible to transfer an audio signal via fourier transformation as a list of values, which are then processed (like adding harmonic multiples of the signal) and then transformed back into an audio signal? Maybe there’s a misconception in my head.
yes, softclip nails it.
there are hundred ways how to build it and i wont take you the enjoyment to find your own way by showing off an example.
however, a good practice can be to apply this kind of effect only to the values higher than 1. (and likewise -1.) an analog mixer also dont distort altready when in the green range. ;)
fourier? there are objects such as [ifft~] and [pfft~], the latter comes with a bunch of special objects which do most jobs you could need in an fft.
Is it possible to transfer an audio signal via fourier transformation as a list of values, which are then processed (like adding harmonic multiples of the signal)
Clipping is also adding harmonics to the signal - the exact nature of the clipping will determine which harmonics (and their magnitude). I certainly don't mean to deter your from experimenting and learning, but if your goal is a principally a guitar overdrive pedal, doing the processing in the frequency domain might be kind of overkill, and you can probably get what you want with a combination of clipping and then maybe some EQ to tame or boost certainly frequency ranges.
This may be of some use to you:
https://cycling74.com/tutorials/frequency-domain-processing-in-gen~-an-introduction
