How to make a leaky accumulator in Gen?
I'm looking for something like += or accum to hold an arbitrary number of accumulated samples. Let's say I want a 1000 sample accumulator, updated every sample. Not a total reset.
The accumulator should continuously remove the oldest sample and add the newest sample, updating the total.
What is the approach here? Codebox, delay, buffer? Perhaps there is something like this already?
Thanks all.
if you don't need to visualize the data, you can use the 'data' op instead of 'buffer' in gen~(and yes, codebox would be ideal because of the for-loop which can iterate over the desired amount of samples)...
...i tried to begin with the "gen~.buffer.sort" example from the "Examples->gen" folder, and am thinking it might be as simple as cutting out the sort algorithm and simply using something like this:
Data src(1000);
History accumulated(0);
....
....
accumulated -= peek(src,dim(src)-1); //if 'data' is empty, this line...
//..will leave 'accumulated' at '0', otherwise...
//..subtracts the final(discarded) sample value.
for (i=1; i<dim(src); i+=1) //<-start count from sample-index '1' not '0'!
{
poke(src, peek(src, i-1), i); //<-shuffling older samps through memory
accumulated += peek(src,i); //<-accumulating all those old values
}
poke(src, in1, 0); //write new input into sample-index '0'
accumulated += peek(src,0); //adding that new input to accumulation
out1 = accumulated;
...then i realized i don't understand your context in full(in particular, where you will get input from(if realtime from an audio signal or shuffling data at a specific rate from some other place, or else polled by specific request such as in the example patch, etc.), so i'm hoping this much can help get you the rest of the way 🍻
Thank you, this does give me something to work with.
I want to fill the leaky accumulator in real time with an audio signal.
My thinking is that until I change the input signal, sig~ 1 with Data src(1000) should keep holding the codebox's output at 1000.
You can see in the screenshot how the codebox behavior differs from normal Gen accum. I ran the patch for a little over a second at a sample rate of 44.1 kHz, which means the value of 57537 is the expected one.
It seems that the for-loop needs adjustment, or there's something else I'm not getting.

oh, feels like i misunderstood you right from the start as you wrote:
updated every sample. Not a total reset.
without a 'reset', i didn't understand how you'd do anything beyond counting the 1000 samples one single time you ran it... if you expect it to count to 1000 then stop, then i guess that's much simpler...
here's a simple bit to do that:
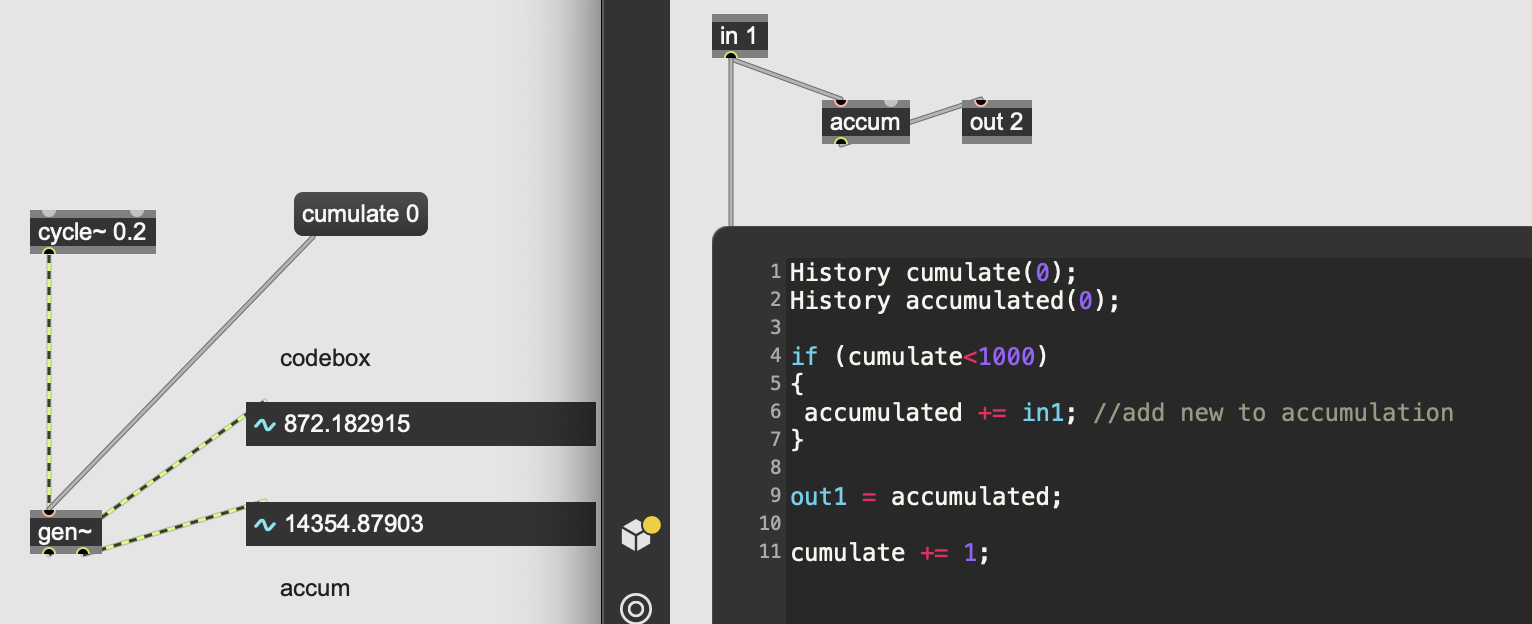
(you can see in the screenshot above, just send a message "cumulate 0" directly to the gen~ patcher from outside to reset the 'cumulate' history object within to '0', which will free the conditional 'if' statement to grab a new accumulation of 1000 samples in real-time audio after that)
before this, i thought you needed the 'data' space to do something else with the 1000 samples collected, seems it can be much simpler than that :)
[Edit: also, just to explain another error i made, when i put the accumulation ('accumulated += peek(src, i)') within the for-loop, it accumulated the 1000 samples within 'data' every sample at sample-rate, which made the output 1000x greater, plus, i didn't need to subtract from the accumulation, etc...
but all that was unnecessary even in principle because we didn't even need to record the history of the entire 1000 samples, just simply accumulate their values for up to 1000]
hope it helps 🍻
Well, that looks similar to a counter with a count limit of 1000. I would say that the earlier code was nearly correct. I suspected that line ('accumulated += peek(src, i)') was causing an issue, but I am still not sure how to get the right behavior here.
The sample length of 1000 is just an example, really it should count n samples based on an external signal through in2.
1000 isn't a maximum count limit or anything. Sig~2 at Data src(1000) should hold the output at 2000, sig~ 3 at Data src(100) should hold at 300. Phasor~ 1 at Data src(100) should have a constantly changing positive output based on what's held in the 100 sample window, but not gradually increasing over longer periods of time.
Also, cumulate, or cumulator is a good name for this object!
1000 isn't a maximum count limit or anything. Sig~2 at Data src(1000) should hold the output at 2000, sig~ 3 at Data src(100) should hold at 300. Phasor~ 1 at Data src(100) should have a constantly changing positive output based on what's held in the 100 sample window, but not increasing over longer periods of time.
this is all an interesting design(i'd only heard of a 'leaky integrator' before, never seen 'leaky accumulator' before except in other contexts where the algorithm is much more complex and doesn't relate to audio necessarily). but it sounds like you're coming up with it as we go(i didn't even realize there would be a sig2 and sig3 etc.). i think i've given enough code so far to get you the full way. i'll leave the rest for others to help with further, but i highly recommend you look through the gen example folder, particularly "gen~.buffer.sort" is where i'm starting from for everything.
best of luck!
Sig~ 2 and sig~ 3 are just theoretical input signals for the purpose of an example. I mentioned them to demonstrate what I expect the output to be based on an arbitrary input.
The codebox only needs in1 for the audio signal and in2 for the sample length, which is currently fixed at 1000.
You are right that 'leaky accumulator' may be unclear. Perhaps 'windowed accumulator,' or simply 'cumulator' is better.
I will look at gen~.buffer.sort to get a better understanding. Thank you!
Maybe what you are looking for is a sliding window sum? So, if the length N is 1000, the algorithm always gives you the sum of the last 1000 samples?
There's an efficient way to do this if N is constant: the input is added to an accumulator (e.g. accum) and also send it into a delay of length N; negate the output of the delay and also add that the the accum. Simply put, your sum adds the immediate input and subtracts the input from N samples ago, which is just 2 operations, no expensive for loops needed.
There's a bit more explanation on this stackoverflow: https://stackoverflow.com/questions/8269916/what-is-sliding-window-algorithm-examples
However this trick doesn't work if N can change dynamically.
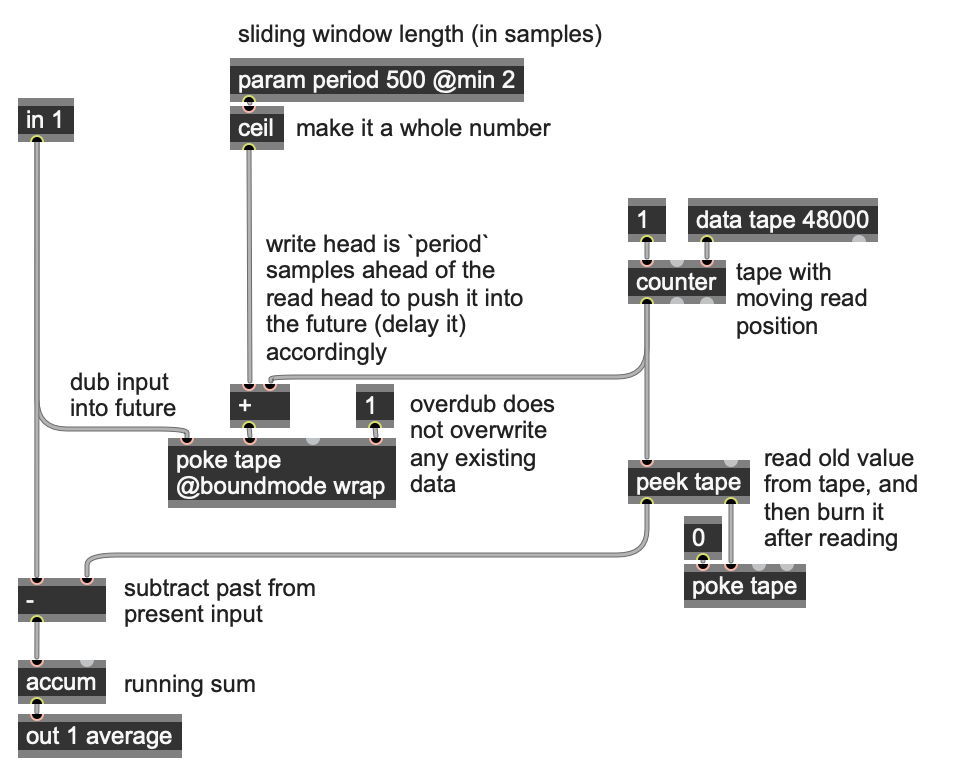
In that case there's still a trick that can be used to avoid making expensive for loops, but it is a bit more fiddly. The basic idea is the same but this time you use a data instead of a delay. The accum input is the new input minus a value read from the data using a moving read index. Once you read a sample from the data , zero that sample using poke, and increase the read index by 1. You also then poke the new input (with overdub=1) into the data N samples into the future (N samples ahead of the read head), so that it will be subtracted out again in the future. This method is basically the same as an overlap-add technique on a circular "tape" buffer.
Why do we use tape overdubbing here not a simple delay? To ensure that even if the period changes, no matter whatever we add in at the input will always eventually be subtracted away again. Overdubbing into the future tape ensures this.
Hey Graham,
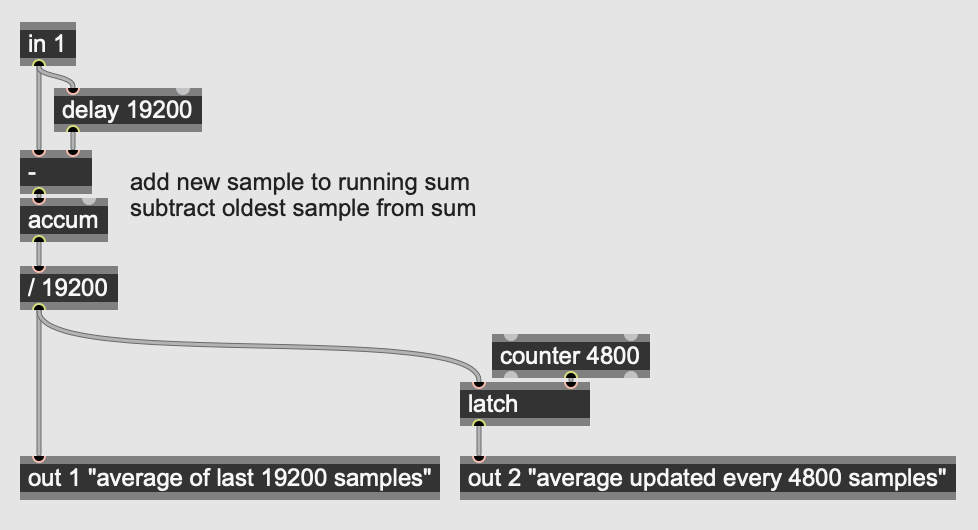
In your example of the sliding window - if I wanted to take a sliding window average of 400ms (19200 samples at 48k) with a 75% overlap (100ms, 4800 samples), would I essentially change the Data tape to 19200, and the period to 4800 then divide the accum by 19200?
The example I posted always outputs the average of the last N samples (where N=19200 in your case), and that average is updated on every new sample, so there's not really a concept of "overlap" at all (or rather, overlap is the maximum that it could be).
Overlap as a concept only really makes sense if you are only periodically updating the average in "frames", which is something some algorithms are forced to do. But a running average can be computed per sample, so there's no need for frames like this.
Please also note the comment up there: if N is a constant, this can be done a lot more simply with just a delay, and accum.
If you really only want to know what this value is every 4800 samples, you can latch it.