FM vs PM in GEN, unwanted artifacts & clicks
Hi
i've been working for some time on a GEN-based, multi operator FM synthesis patch. In order to avoid accuracy & feedback issues, I've used the PM version of FM, where the modulators' outputs are summed to the phase of the carrier. When modulating the FM indexes, i found out i get very nasty and audible clicks. Wether i use control rate modulation (i.e number boxes) or signal rate modulation (i.e curve~ envelopes, LFOs) doesn't change a thing to the problem, except maybe that smoother signals like cosine LFOs are less prone to clicking than steeper signals like ramp LFOs (which won't come as surprise to anyone, of course).
So I've run tests to compare a "traditional FM" algo (similar to the "simpleFM~" MSP abstraction) and a PM algo, and to my big surprise the PM algo is the less accurate. This is very unexpected to me since most available litterature on FM synthesis advises to go the PM way. And AFAIK, PM is what Yamaha used in the whole DX line.
Attached to this post is a patch to demonstrate the issue: it's based loosely on an FM patch someone posted a while ago in this forum. There's a number box in the upper left corner to choose between trad. FM or PM. The modulation index comes from a looping curve~ envelope with adjustable parameters. In case the clicks are not audible enough, they are VERY visible on a sonogram, as is the difference between the 2 algos.
Any help on this would be very appreciated. Thanks by advance
Best regards
Lionel
Bumping this thread, in hope someone with more DSP knowledge than me passes by
After searching in the forum i found an old thread about the very same issue:
https://cycling74.com/forums/cycle-cos-pm-vs-fm
This was 10 years ago with MSP objects but with GEN you'll get the exact same result.
I understand it has to do with sudden phase increments causing a click in the carrier but it's very annoying, because you can't implement FM feedback correctly without phase modulation.
Makes me wonder how the people who designed the old Yamaha hardwar dealt with this, or even more recent software synths (FM8 & al.)...
Hey Lionel. I looked at your patch and took the liberty to remodel it. I didn't really have the time to look at exactly what was causing the clicks but I suspect it had to do with the way the Phase Mod algo was implemented.
Here are a few guidelines on how to avoid clicks in Max from my own modest experience :
1) Always use an audio smoother if you are using control values to change parameters
2) For percussive sounds, the max envelope generators (curve, line) are perfect. However, for synth leads and pads, I tends to add a slide object just after the curve~ or line~. Usually i use the gen~ native version of the object with a value between 0.5 and 1.5 milliseconds - don't forget to translate to samples - for in2 and in3.
3) Don't be surprised if waveforms other than triangle and sine produce clicks => an audio smoother or a slide object can also help in this case
Here's the patch, tell me what you think ;)
Hi Quasar
thanks a lot for answering, appreciated.
Nice rework of the patch, i know i didn't put enough time into it cause it was meant for testing but your UI makes it a lot more usable.
I'm well aware of the problems when using control rate or even signal rate stuff, so i've already been trying out various smoothing options, either onepole LP like you do, smoothstep~ in MSP or slide in GEN. After some experiments with the curve~ & PM combo, i'd say you need about 400 sps. of sliding to get rid of audible zipper noise, which is about 10 ms worth of latency at 44 khz. That seemed a lot to me if i was going for sharp transients with a very steep envelope, but then i might be wrong.
I'm no DSP expert but i understand the difference between the 2 algos has to do with integrating vs. differentiating (ie frequency vs phase), and with quick changes in phase causing a discontinuity in the waveform. I've been trying various workarounds but as soon as you touch to the phase angle in one way or the other, you'll get clicks. So i wonder how professional programmers dealt with it in available software / hardware.
Do you think there's some param smoothing going on under the hood, or maybe some magic DSP trick only known to a happy few ?
Best regards
10ms of smoothing for the slide in and out values does seem quite high.
If you look at my version of the patch I'm only using 1.25 ms of smoothing for the gen slide object and, to my hears at least - it's the perfect balance of percussiveness. Also, the sliding time is definitely not equal to latency. Slide should actually be seen as a sort of filter which smoothes the edges by filtering them in a logarithmic way.
Another thing, usually in FM Synths, the index envelope is in some way related to an amplitude envelope. I think in your first patch there was no amp envelope at all which made the phase changes introduced by the curve envelope's transient even more noticeable I think.
Hi
i looked at your patch again and the main difference is in the amp envelope, indeed.
There's no real difference in the phase mod. implementation. If i remove or modify the amp envelope, the clicks are back.
It was part of my intention to dissociate both envelopes in order to get evolving timbres independantly of amp., but maybe i was expecting too much of this method.
Thanks again
Hi
re-upping this thread because i finally found a solution (it was given to me by someone from the kvr forum)
You just need to latch the modulator to the carrier's zero-crossings, which is very easy to do in GEN.
Just in case someone stumbles upon the same problem, here is a modified patch with various options to compare the outputs (FM, PM without declicking, PM with declicking).
Thanks a lot ! Thought about zero-crossing in granular contexts but never in this one.
Hey @lionel I didn't need the latch because im just doing 2 free running oscillators (cheers for uploading btw :D) but I liked the way you patched FM better than the built in examples. Just curious... im assuming those gen patches called 'firlp3p' are a 3 pole low pass filter, whats the cut off set to?
My patch is 2 oscillators with wavefolders that FM & AM each other and you can cross fade between each osc. Sounds pretty kewl :P very loosely based on an instruo Cs-L
Hi
which examples are you refering to ? AFAIK there's only the simple FM patch in the tutorial section, which is strictly MSP. In my opinion GEN is the way to go to implement proper phase modulation. Also worth mentioning is the modfm patch from the GEN example files (very inspiring one).
These firlp3p aren't of my own making, you would have to ask Quasar (see above). I guess you could compute the actual cutoff from the filter coefficients, but i don't think it's so important. The way i see it, these things work as moving averages, they're meant to smooth out sharp discontinuites and to avoid part of the nasty aliasing in the feedback path.
Free running oscs are cool for some applications, not so much for others. Sometimes precise phase control between the operators is key. That's where GEN comes in handy.
You can make a decent square wave using a pair of suitably dephased operators in a 2:1 ratio, see here for example:
https://www.youtube.com/watch?v=q3fQDePuaS8
As far as the firlp3p abstractions are concerned they are indeed meant to smooth out the spectrum if phase modulation feedback is used. To be honest I would not be able to tell you the exact cutoff since I "borrowed" the abstraction from Native Instrument's Kontour Reaktor Core code. I tried both with and without this abstraction the PMFB synthesis methode and it always sounds better IMO with the smoothing.
@Lionel/@Quasar this patch sounds incredible, thank you for sharing! Digging in.
Yes, actually quite a lot of algorithms sound better by latching parameter changes at zero crossings (or when modulating derivatives, latching at peaks/troughs, where the slope passes through zero). [latch] is one of my most-used operators.
That's a nice trick to do a zero crossing detection: `src * history(src) <= 0`, very clever; If the sign of the current and previous samples are different, it outputs true (pulse). I usually do `change(src > 0)`, which is 1 on rising crossings and -1 on falling crossings, 0 elsewhere.
Regarding the various smoothing operators: clearly when driving from a control rate parameter, some degree of smoothing is often desirable. This simple old history/mix combo (cheap onepole) is easy to reach for, but the coefficient needed really depends on the block rate. These days for some applications (e.g. where I know the range of output is bounded) I have sometimes been opting for rampsmooth-style filters; these essentially limit how fast the output can rise or fall to the target. The downside is that this curve can sometimes be sharp edged (a refinement is to pass it through a sigmoid type shape, or something toward a blep-style step), but the upside is that you can effectively bandlimit the modulation, and moreover it works regardless of block sizes.
BTW the frlp3p abstraction code was a bit hard to read as it was; I patchified it and it looks a lot clearer to me this way:
Graham
@quasar
iirc lowpass smoothing was used in the original Yamaha DX hardware
don't know about more recent software/plugin implementations though
@graham
lol at that 0-crossing thing, i had no clue how to do it so i drew it on a piece of paper, looked at it stupidly for a while and came to the conclusion that (+) x (-) = (-)
gen is ace for these little arithmetic tricks
So much problem solving at so little cost...
your version is better though because it gives you the direction of the change as a bonus
Interested in seeing what you mean by "rampsmooth style filters" if possible
thx
More exploring. I thought it was very helpful how that patcher shows how similar the two algorithms are, and where their differences lie.
It occurred to me that they could be merged to some degree, in a way that one could cross-fade or blend between FM and PM. So first, I tried to port over the feedback and latching sections from PM to FM. Adding the latching to the FM side didn't seem to change the sound, so that seemed harmless. The modulator feedback path was relatively straightforward. I tried a few variations for where to send the carrier feedback path, but honestly it seems to be more interesting as phase modulation than frequency modulation, so I left it as is. Then I punched in controls to enable depth of FM and depth of PM, which I ran through a poltocar so you have independent control of a) modulation depth and b) FM/PM mix. This isn't as significant as I expected. Playing around, I find there's not a huge difference between FM or PM until the modulator feedback is enabled. But, it's another modulation point at least.
I also turned the carrier into a quadrature oscillator, which adds some nice stereo; and turned some parameters into signal inputs for modulation.
It would be nice to merge some of these ideas and turn it into an example included in Max if that would be OK with everyone.
There's also an example of ramplimited smoothing in there (just after the poltocar).
Hi Graham
nice refinements, thanks !
No problem for me to include it in the examples section, i think it would fill a gap.
In theory there should be no difference between PM & FM, one being the derivative of the other. In practice : not so simple anymore... & even less so when feedback comes into play.
i confirm no latching is needed in the FM case. Never heard a click there, even with very fast percussive envelopes. The downside with FM is that the feedback is pretty much useless (for my taste at least, some people may prefer the inharmonicity for certain types of sounds). This was the main reason for me to go away from the simpleFM patch. If you want to replicate the "classic", harmonic feedback sounds, PM is required.
Also, PM sounds a bit more "aggressive" to my ears, for lack of a better word, even with de-clicking enabled.
Regarding the dcblocker: i'm clueless, sorry... dcblocking is one of those things i never seem to get right.
Great job for those additions ! I agree this patch would make a nice addition to the gen~ Examples section ;)
I might try and implement the zero crossing latching again in my patch now and see what effect it has with both oscillators feeding back on each other. Also btw, just measuring with noise it looks like that filter is roughly a 12khz lowpass.
Hi Robert
As long as you don't put the mod depth under heavy and fast modulation, the zerox latch shouldn't have a big influence on the sound.
IMHO lowpass smoothing would be more critical: with increased mod depth, PM cross mod quickly produces very nasty aliasing, peaking at approx. SR/4 if i'm not mistaken.
One nice trick if you haven't tried it already is to slightly detune one of the oscillators. Then try increasing the frequency multiplier of the modulator for example.
@raja
i'm not a filter specialist, but AFAIK the filter coefs are linked somehow to cutoff frequency & resonance, so computing the exact cutoff should be possible. Maybe someone more knowledgeable can tell the filter type and the associated formulas ?
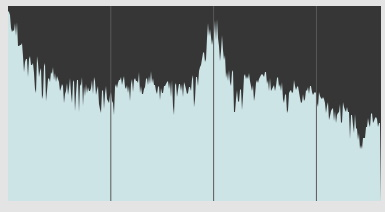
Meanwhile i've been doing a few little experiments on the side, using PM cross mod between 2 oscillators to deliberately generate aliasing, here are 2 spectrograms:
1. C/M ratio 1.0, mod depth(2-->1) = 0.65, mod depth(1-->2) = 0.1, no smoothing
1. C/M ratio 1.0, mod depth (2-->1) = 1.3, mod depth (1-->2) = 0.1, lp3 smoothing on both oscillators
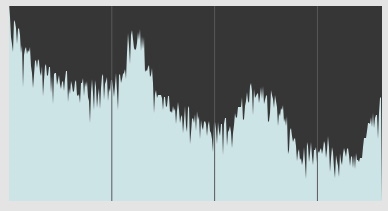
Notice the difference of flavour between the 2, the aliasing peaks occuring at different frequencies. The position of these peaks doesn't vary if you change the pitch or the samplerate.
Also, notice my choice of a higher mod depth in the second case (X 2). The LP3 smoother mostly acts as an attenuator of the mod depth, so you get a little less of the higher harmonics. But you can always compensate for the loss of bandwidth, and increase the levels to the point where you get aliasing anyway...
I too was under the impression that it should be samplerate dependant, seems to make sense since it changes nyqvist freq., but apparently not.
The filter type is definitely lowpass but the exact characteristics depend on filter topology and coefs.
The bottom line is : there is no cheap way of getting rid of aliasing, the only thing you can do is to
reduce the mod index as the pitch increases, thats why keyscaling is included in ost commercial products ...
yeah nice one peeps. yeah I imagined there would be no easy way to find the cutoff unless you knew how to make a filter from scratch (and that knowing the filter coefficients may not make it reverse engineer-able), either way we know its something like a 3 pole low pass (18db/oct probably) somewhere around 12khz and does very little to stop aliasing and more to improve the useable range of feedback/modulation amounts. In my patch (recursive phase modulation between 2 oscillators followed by wavefolding) I had to upsample 4x to reduce the aliasing to a useable musical level, normally I'd only have to upsample by 2, so loads of upper harmonics and partials getting flown around which is great haha.
"there is no cheap way of getting rid of aliasing" -- indeed!
For things like AM/RM, you may be able to (to some degree) predict what the sideband frequencies might be if you know the components of the carrier & modulator (by sum and difference), and with that knowledge you can attenuate/filter them accordingly to prevent aliasing. Simple case: if both carrier & modulator are sines, you just need the fundamentals, take the (absolute) sums and differences of the fundamental frequencies, and if either starts getting close to Nyquist then attenuate the modulation toward zero. If either waveform is more complex, you need to know more about what the harmonics are (frequency and amplitude), but the same kind of logic can apply.
But when modulating FM/PM the situation is pretty much a nightmare as far as I understand it -- computing the frequencies isn't so bad, but computing the amplitudes is complicated: https://ccrma.stanford.edu/software/clm/compmus/clm-tutorials/fm2.html
Still, it might be fun to explore some ways of modulating feedback modulation according to predicted frequencies of the output... :-)
@graham
not very familiar with AM but with complex FM, computing of amplitudes is a mathematical nightmare as you say. Adding cascades of modulators and feedback makes it worse. Much cheaper to generate these things in practice than it is to analyse them in theory, but that's the beauty of it.
Simple 2 operator configurations are still manageable to some extent, see here for a nice application :
https://www.semanticscholar.org/paper/Synthesis-of-Quasi-Bandlimited-Analog-Waveforms-3%2F-Schoffhauzer/ee7aede98685275144487265045ad08ce90c2ed5
but anything beyond that gets out of control very quickly.
Exponential scaling of mod index mapped to midi note seems to be the best option. Then for each operator, manual fine tuning of breakpoint & coefs to taste... Might even depend on the sort of envelopes you are using & the type of sound you are after.
I guess by the time we have enough CPU to run everything at 192 khz, we'll laugh at ourselves for having had these discussions :-)
Maybe... or maybe we'll just want moar modulation!
I do have the intuition though that if we had a bit more information about what we are modulating and modulating with, there ought to be some predictive capacity we could lean on to filter earlier in the chain when needed. I wonder sometimes if these things would be easier if we were working with complex numbers rather than reals (ha, or even quaternions...). But that's just probably naive me, I wasn't trained as a signal processing or acoustic engineer, I really don't know what I'm talking about in these waters.
Pushing the aliasing out of the audible range would help but I'm not sure i need more modulation really.
Or maybe you speculate that the human hearing will evolve beyond the 20khz limit ? ...
Joking apart, there's a point where i think a tad of EQing might be more helpful, just to reduce or enhance the higher harmonics for example.
As for bandlimiting & al: i've been dabbling a bit with BLEP but the underlying math is way over my head.
And when it comes to FM, i have a feeling that dealing with bessel functions in real time wouldn't be computationally cheap...
