Husserl tutorial series (3). Wavetables and Wavesets

A more practical tutorial on wavetables, and wavesets in gen~. Tutorials in this series:

1. Designing a good LFO in gen~ Codebox: https://cycling74.com/forums/gen~-codebox-tutorial-oscillators-part-one

2. Resampling: when Average is Better: https://cycling74.com/forums/gen~-codebox-tutorial-oscillators-part-2

3. Wavetables and Wavesets: https://cycling74.com/forums/gen~-codebox-tutorial-oscillators-part-3

4. Anti-Aliasing Oscillators: https://cycling74.com/forums/husserl-tutorial-series-part-4-anti-aliasing-oscillators

5. Implementing Multiphony in Max: https://cycling74.com/forums/implementing-multiphony-in-max

6. Envelope Followers, Limiters, and Compressors: https://cycling74.com/forums/husserl-tutorial-series-part-6-envelope-followers-limiting-and-compression

7. Repeating ADSR Envelope in gen~: https://cycling74.com/forums/husserl-tutorials-part-7-repeating-adsr-envelope-in-gen~

8. JavaScript: the Oddest Programming Language: https://cycling74.com/forums/husserl-tutorial-series-javascript-part-one

9. JavaScript for the UI, and JSUI:<a href="https://cycling74.com/forums/husserl-tutorial-9-javascript-for-the-ui-and-jsui"> https://cycling74.com/forums/husserl-tutorial-9-javascript-for-the-ui-and-jsui

10. Programming pattrstorage with JavaScript: https://cycling74.com/forums/husserl-tutorial-series-programming-pattrstorage-with-javascript

11. Programming pattrstorage with JavaScript: https://cycling74.com/forums/husserl-tutorial-series-programming-pattrstorage-with-javascript

12. Applying gen to MIDI and real-world cases. https://cycling74.com/forums/husserl-tutorial-series-11-applying-gen-to-midi-and-real-world-cases

Wavetables and Wavesets

So first there is a confusion about the difference between wavetables and wavesets. I am not a wavetable guy but here's the gist of it:

• WAVETABLES usually play sampled instruments, although some play natural or synthesized sounds. Perhaps the best wavetable implementation was by Creative Labs, which pioneered the technology, and made many enhancements now sold commercially for thousands of dollars, and totally pirated by everyone, including Microsoft for its free MIDI GM player on Windows. Creative originally had some enhancements that have mostly been dropped, including by Cycling 74, for defining the attack segment, main loop, and release segment within a single sample. The difficulties of defining breakpoints between the segments on zero crossings was too much for the majority of users, who typically don't have attack or release segments at all and simply loop a simple sample.

• WAVESETS define a sequence of oscillations which can be swept through to recreate sounds like filter sweeps, pioneered by Wolfgang Palm, and who had extensive patents on the technique. But by the time I asked his permission to use wavesets in my own software, he had given up defending his patents which also had been pirated worldwide. Which all leads to my second most important advice for sound developers, after making stuff that's reusable, don't even bother trying to stop people stealing it beyond asking for a registry key, which most customers who will pay will respect. Otherwise, music software is one of the most corrupt businesses in the world. It all gets stolen no matter what you do, usually by people in another country. People with integrity will pay for it, and that's going to be about 0.1% of the people who try any free versions. I'm not the only person to say that.

Both wavetables and wavesets are similar in that they play presampled sounds, which are played back at different rates depending on the desired note pitch (usually the pitch of MIDI notes on an equal-tempered scale). Wavesets tend to work at any pitch, but samples of real instruments infrequently work well across the original instrument's full range, so they are layered and cross-faded across 'zones' to provide better sound simulacra. That was also part of the original soundfont design, and it turned into a reasonably lucrative market for a while, but as with all such things it is now flooded with too much of much of the same and quite a bit that is already free, so I am in no way encouraging anyone to think they can make money at it. At all. I had to say that at least once in this series.

Using polybuffer~ for samples.

Max's polybuffer~ object is a recent addition to the Max object palette that allows one object to contain and provide access to an array of buffers. This is useful for layering sounds, as in this example from Sam Pearce Davis:

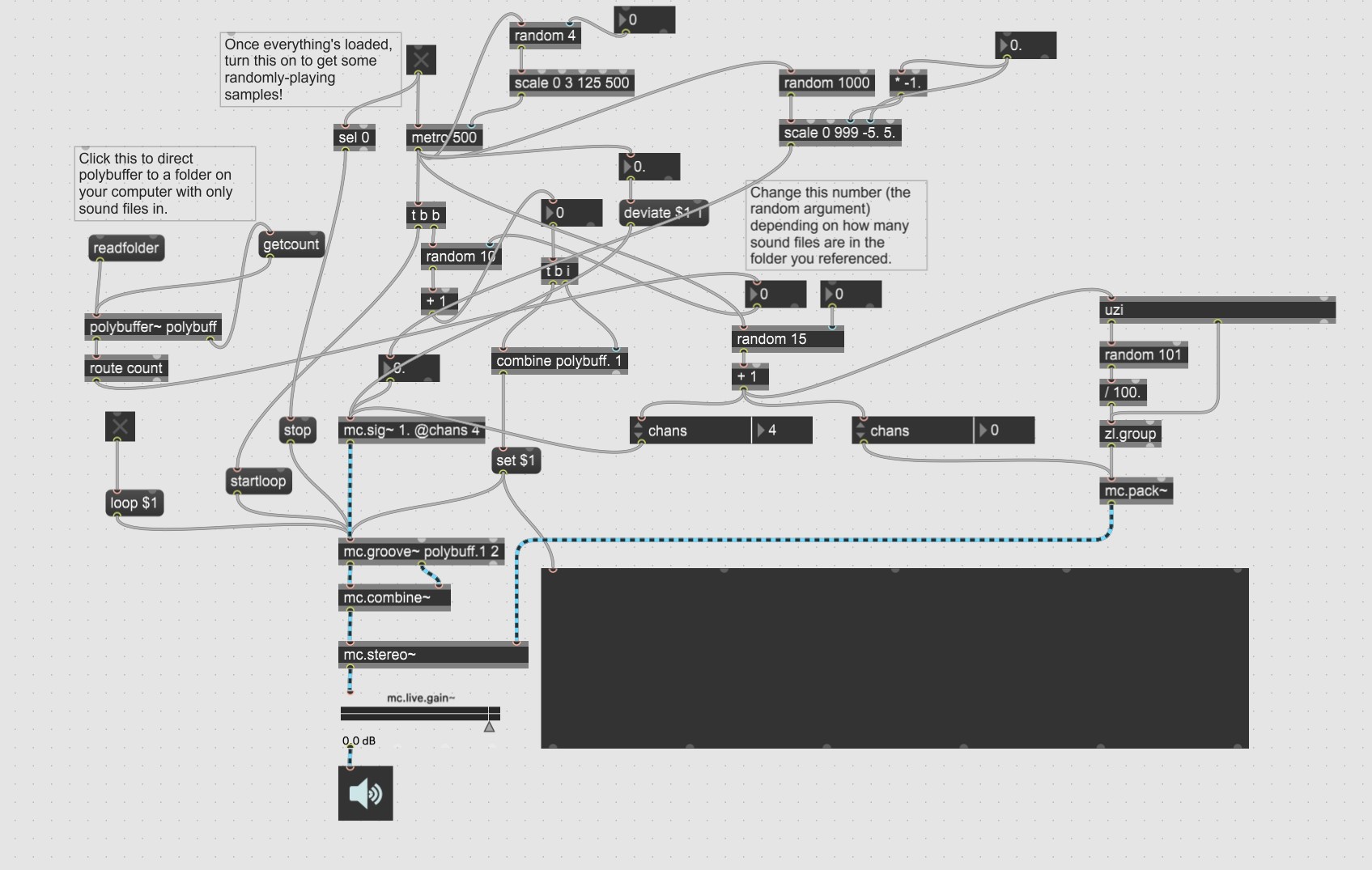
The polybuffer~ data is available in gen~ as buffers, for which I will provide a self-generating example in the forthcoming days.

Playing Single-Cycle Wave Samples

To play your own samples in gen~, there is a new built-in function added in Max8 called [wave()] to simplify it, However if you know the startpoints and endpoints for the loop, you can precalculate peek statements, which is more efficient. But you do have to be careful, if you are looping over the loop boundaries, to get the right samples from the beginning and end of the loop for interpolation, or you will get clicks. In my case, I had a buffer containing a set of 128 single oscillations 256 cycles long each, in 50 banks. I catenated all the waveforms I wanted into a single-channel .wav file, so I could step through it to the individual waveforms in the set, rather than switching between thousands of soundfiles. Then I made this to interpolate arbitrary points within each of the 256-sample loops.

waveset(ramp, wave, waveset){
    Buffer wav("wav");
    x     = floor(wave) * 256;
    y     = x + 256;         
    if(y  > 32768)  y -= 32768; 
    r0    = ramp -1;         
    if(r0 < 0  )   r0 += 256; 
    r1    = ramp +1;        
    if(r1 > 256)   r1 -= 256;
    r2    = ramp +2;         
    if(r2 > 256)   r2 -= 256;
    x = interp(fract(ramp),    wav.peek( x + r0,   waveset),
        wav.peek( x + ramp, waveset),
        wav.peek( x + r1,   waveset),
        wav.peek( x + r2,   waveset), mode="spline" ) ;
    y = interp(fract(ramp),    wav.peek( y + r0,   waveset),
        wav.peek( y + ramp, waveset),
        wav.peek( y + r1,   waveset),
        wav.peek( y + r2,   waveset), mode="spline" ) ;
    return x + (y - x) * (fract(wave));

I'll explain it a little, although the above should be pretty self explanatory. It uses the gen~ built in [interp()] function, because I don't think I could write a better interpolator for arbitrary points than Cycling74. The function receives a ramp of the desired frequency that runs between 0 and 256, rather than 0 and 1, because that's the length of my sample set for each cycle, and that results in the simplest maths to calculate the intermediary points.

But at the ramps beginning and end, any number of the individual samples could wrap to the other end of the loop. Cycling74's spline interpolation requires two points a cycle after the target, and two before, one of which is the original sample point. So this code wraps the index of the other three sample points within the 256-sample window, fetches them with individual peek statements, then interpolates between them using gen~'s built in [interp] function.

I could want to mix any one of the wavesets with the set before or after it in the sequence, so I do the same for four samples again for the corresponding point in the next or previous wave, and linearly interpolate between them (because as the two sets are different waves, splines couldn't do much better):

Optimizing the Above Function

Of course I was lazy writing that, and even though we had a lot of discussion about how to do this during Max6, no one has ever told me I should have used ternary operators, or to interleave statements so there's some time for the previous statement to get through the FPU pipeline before its result is needed. In fact, when I got to thinking I better do that today, I realized I should write a bit more tutorial on it, because I already got a lot of questions on it as it was, and people would otherwise not understand why I changed this at all, which actually is about ~.5% faster on my 4GHz 6700K-i7 for a single voice. I hope to run 64 voices, so every bit helps:

waveset(ramp, wave, waveset){
    Buffer wav("wav");
    x   = floor(wave) *256;
    r0  = (ramp -1 < 0) ? ramp +255 : ramp -1   ;
    y   = (x > 32512)   ? x -32512  : x    +256 ;
    r1  = (ramp > 255)  ? ramp -255 : ramp +1   ;
    r2  = (ramp >254)   ? ramp -254 : ramp +2   ;
    i   = fract(ramp);
    a = wav.peek( x + r0  ,   waveset);
    b = wav.peek( x + ramp,   waveset);    
    c = wav.peek( x + r1  ,   waveset);
    d = wav.peek( x + r2  ,   waveset);
    e = wav.peek( y + r0  ,   waveset);
    f = wav.peek( y + ramp,   waveset);
    g = wav.peek( y + r2  ,   waveset);
    h = wav.peek( y + r2  ,   waveset);
    x  = interp(i, a, b, c, d, mode = "spline");
    y  = interp(i, e, f, g, h, mode ="spline" );
    return x + (y - x) * (fract(wave));
}

You might notice, while I rewrote it to remove statement interdependencies and interleaved the OTHER statements as described as best practice before, the peek and poke statements are still as purely sequentially as most frequently occurs. This is because I've been told Max loads 32 words of a buffer~ at a time, so the buffer data is already in the primary cache after the first peek. It also helps to keep your buffer accesses aligned within 32-word boundaries. Of course, as with Param evaluation mentioned in Tutorial One, the actual fetch size might be dependent on your audio driver settings. But I do know, if your peeks and pokes of shared buffers are scattered through your code rather than sequential, your performance is abysmal. The impact is less for local data() reads and writes.

Removing Code Dependencies

Really I should have emphasized this before, particularly because 'removing code dependencies' was somewhat of a catchphrase in silicon valley in the 1990s. The first version of the above example causes loads of FPU pipeline stalls, because so many of its single statements require the results of the prior statement:

y = x + 256;
if(y  > 32768)  y -= 32768;      
r0 = ramp -1;
if(r0 < 0  )   r0 += 256;
r1 = ramp +1;
if(r1 > 256)   r1 -= 256;
r2 = ramp +2;
if(r2 > 256)   r2 -= 256; 

Whereas my first version might be more akin to how you figure out it works than an optimized version, it's not a very good code design. It's a simple matter to rewrite the conditional expressions so that the CPU can work on consecutive statements without waiting for the result of the prior one, and to use ternary expressions (as explained in Part One of this tutorial series):

r0 = (ramp -1 < 0) ? ramp +255 : ramp -1;
y  = (x > 32512)   ? x  -32512 : x +256 ;
r1 = (ramp > 255)  ? ramp -255 : ramp +1;
r2 = (ramp >254)   ? ramp -254 : ramp +2;    

(As described in Part One, the less frequent occurrence of the wrapping back to the beginning of the waveform should be the first, or positive, evaluation in the right-hand pair of alternative calculations. The far more frequent incremental step to the next point in the waveform should be on the negative result of the conditional test, because modern CPUs precalculate the negative results of conditional tests while the condition is itself still being evaluated. )

In this optimized example, the ternary comparisons work on predetermined constants, rather than requiring a sequential subtraction or addition of ones to the base wavepoint. That is the point of 'removing code dependencies:' to enable better execution on superscalar CPU architectures, which attempt to execute more than one instruction per clock cycle, by making consecutive statements independent of each other. it's usually not so obvious what will be the optimal structure until after the code is first written, and usually it takes a couple of passes to make code so optimal, because the possible optimizations aren't so apparent while you're still working out how to write the function.

When superscalar pipelining first appeared on the scene, tech companies put an enormous amount of investment and hired loads of software developers to remove code dependencies. More recently, fanaticism about object-oriented programming (OOP) has kind of pushed the benefits of such optimizations off the sidelines. So you could probably repurpose your skills in audio software optimization to get a lot of good-paying jobs in the future. There's a lot of code dependencies that have popped up again in modern software, which you could persuade companies need fixing!

Anyway, that covers the majority of issues with writing good code for floating-point operations. The next tutorials will be focusing on audio functions themselves. Have a good weekend everybody )