Unexpected floating-point > (greater than) object behaviour with floating-point number box input
I am experiencing the following unexpected behaviour (8.1.11 on Mac 10.14.6):
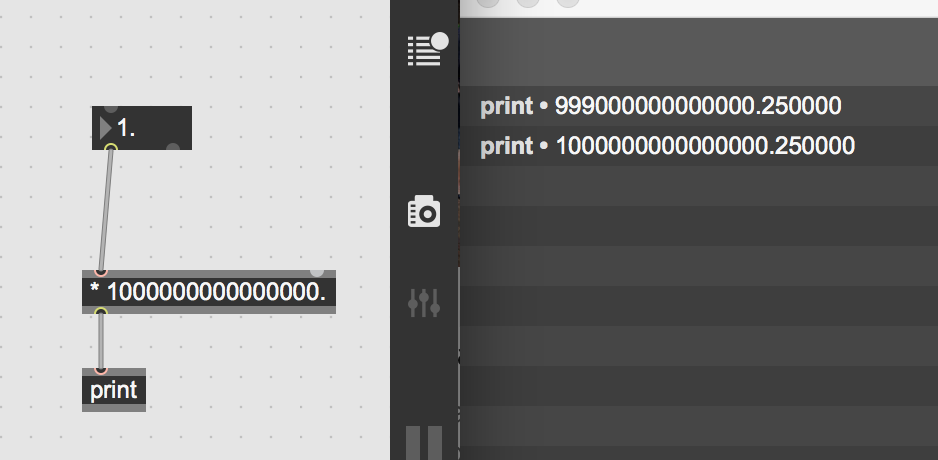
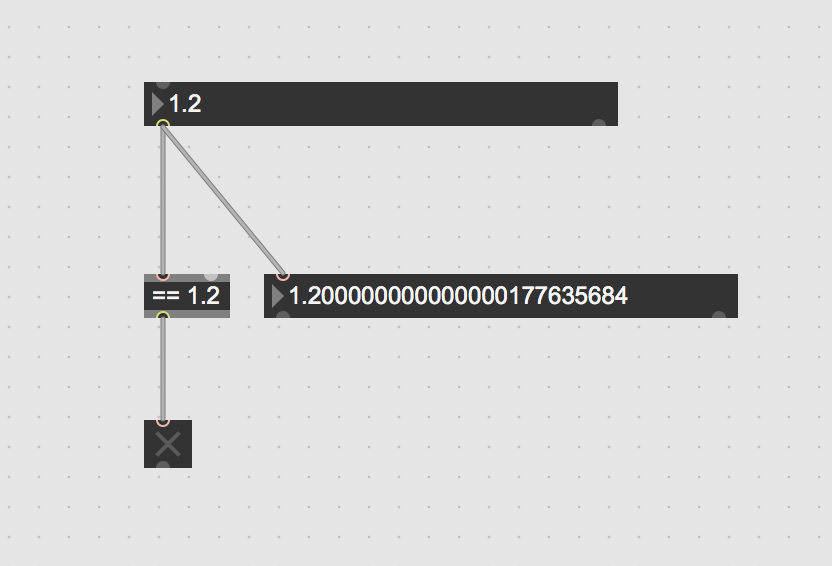
when I connect a floating-point number box to a ">" object with 1. as its argument and click-drag the number box from 0.99 to 1., requesting the 1. > 1. comparison, the output unexpectedly jumps from 0 to 1.
The same thing happens when coming from 1.01 down to 1., and it seems to actually happen for every manual click-drag to any floating point argument from a two decimal (or smaller) place distance.
I tested the same simple patch on an old Max 6 version and there the 1. > 1. after the click-drag resulted in the expected 0.
I ran into this issue while testing an object that I'm coding in Xcode, which includes float > comparison code, using a float number box as input. It seems that the incoming double is not actually 1. but 1.00000000000000022204460492503131...
Here is a simple > patch:
i´ve experimented a bit and i am also managed to get "true" from it when coming from below 1.0
it starts to happen as soon as you move the second or higher digit behind the comma.
Exact, but also coming down from above 1.0.
No problem with > 0.
if you bang it again after it happened, it remains at that ghost value and still returns the same wrong result.
changing how many digits are displayed doesnt help either.
it must have something to do with the fact that the mouse input triggers a multiplication, like a wrong scaling of the mouse coordinates.
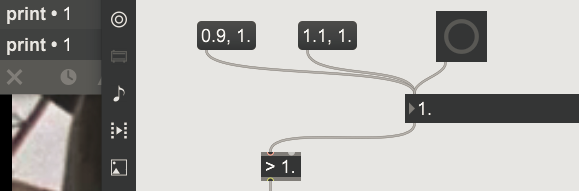
that makes sense.
but i wonder then why that same input mechanism doesn't cause problems with other operators?
if it does not get the 1.0 right but sends one value higher than 1.0, you will only find an issue with > and ==.
most of these bugs are annoying, but this one is somehow interesting. i mean how it can display the correct value when in fact it is a different one?
i often have trouble with things like that when creating custom GUI elements. nice to see that i am not more dumb than cycling. :P
could you notice any difference between using digit #2 and digit #7?
I think I found a similar thing in gen~ a while back. Take a look at the the attached. I may have done something stupid, but I don't think so...
That indeed looks like the same issue. If you take out the absdiff and do the straight <= comparison with a 1. into the right inlet and then creep up or down to 1. with the float box going into the left input (click-dragging the second digit behind the decimal point) you see that 1. <= 1. gives 0.
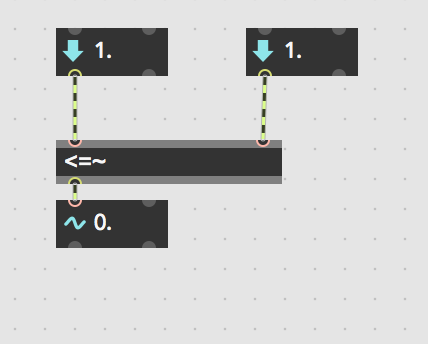
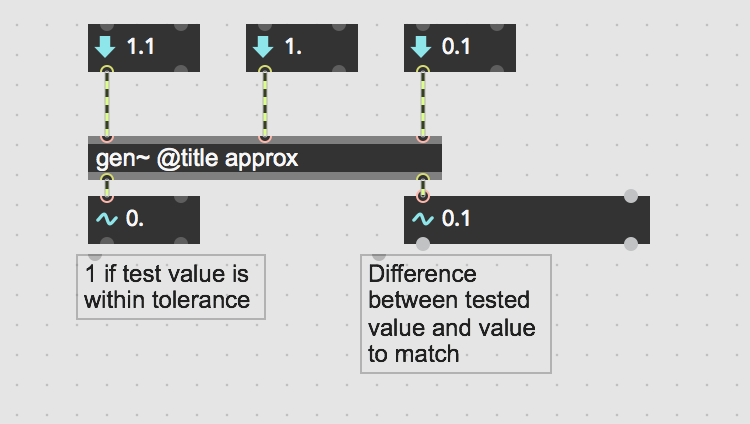
Right! Weird. Have you reported this as a bug to cycling? I reported the gen~ one but it doesn't seem to have been addressed yet.
Reported now.
And the above number~ into <=~ example gives the correct output in Max 6.1.9
i would really like to know why it does not happen with the first digit.
This is all down to the way floating point numbers work, which accounts for almost every representation of non-integer numbers in most software today.
The short version: don't rely on floats for doing integer equality or comparison tests. (And generally don't use floats for equality tests at all.)
See here: https://floating-point-gui.de/errors/comparison/
Also specifically about comparison: http://www.cs.technion.ac.il/users/yechiel/c++-faq/floating-point-arith.html
Why are floating points so weird? https://dev.to/alldanielscott/why-floating-point-numbers-are-so-weird-e03
A dry version: https://floating-point-gui.de/formats/fp/
Visualization: http://evanw.github.io/float-toy/ or https://float.exposed/0x40490fdb
A really nice deep dive for those who want to really understand this: https://ryanstutorials.net/binary-tutorial/binary-floating-point.php
Or for a drier material: https://en.wikipedia.org/wiki/Floating-point_arithmetic
AND... note that gen~ uses 64-bit floats throughout. 64-bit Max should also be using 64-bit floats throughout (but any of you still using 32-bit Max may also be having some floating point oddities crop up as the 32-bit floats get converted to 64-bit inside gen~ and back to 32-bit outside.)
So, even if the number box displays a "1." the underlying number might be slightly more or less than 1., to a degree beyond what the number box can represent.
So here's the 3 nearest numbers to 1.0 in a 64-bit double:
https://float.exposed/0x3fefffffffffffff = 0.999999999999999888978
https://float.exposed/0x3ff0000000000000 = 1.00000000000000000000
https://float.exposed/0x3ff0000000000001 = 1.00000000000000022204
Any number between these values will be quantized to one of them.
Any display of these numbers without all 22 digits will inevitably round them accordingly. The first one of these will be displayed as "1.0" unless you can display the number with all 22 digits of precision; any less and it will naturally round to 1.0 in the display. The third one needs 18 digits to display as anything other than 1.0.
All numbers are quantized somewhat.
Moreover, even some apparently "simple" numbers can't be accurately represented as floats. Even something as simple as "0.1" isn't representable; the nearest two are:
https://float.exposed/0x3fb9999999999999 = 0.0999999999999999916733
https://float.exposed/0x3fb999999999999a = 0.100000000000000005551
So, adding two apparently "simple" numbers can easily end up producing something that isn't simple -- such as an integer that's not quite an integer anymore.
And so, testing for equality, or comparison, can lead to confusing results, as what looks like two numbers that are equal might in fact be two numbers very slightly apart.
Graham
Thanks for those references and explanations!
I would be interested to know how this behaviour was prevented in earlier Max versions.
The output of the floating point number boxes are the result of a floating point calculation when set by click dragging. But I can imagine that the same part of the code that determines the fact that there are no digits intended to the right of the decimal point in the number box could ensure an exact whole number floating point output, if such a thing actually exists, the https://float.exposed/0x3ff0000000000000 = 1.00000000000000000000 let's say.
If the comparison 1. > 1. can have the right outcome when the 1. is typed into the box but not when the 1. is reached by the intended use of the interface element perhaps there is a solution to be found in the implementation of the interface element.
"So, even if the number box displays a "1." the underlying number might be slightly more or less than 1., to a degree beyond what the number box can represent. "
this does not explain why moving the mouse does not let you reach the number you want - or why it used to work in older versions of max.
i can expect that when i "substract 1/100" at the second digit behind the comma from 1.01000000000000000888, that i end up with 1.00000000000000000000, and not with 1.00000000000000022204
Regarding earlier Max versions, google shows that people have been tripping up on floating point weirdness for more than a decade. https://www.google.com/search?q=site%3Acycling74.com+floating+point+precision
Just a reminder -- this isn't anything specific to Max. It's the nature of floating point numbers as used in nearly all software applications dealing with non-integer values. (If the computer science ancients had settled on using ratios rather than binary exponents, we'd be complaining about a different set of issues).
As far as I can tell, the interface works as expected:
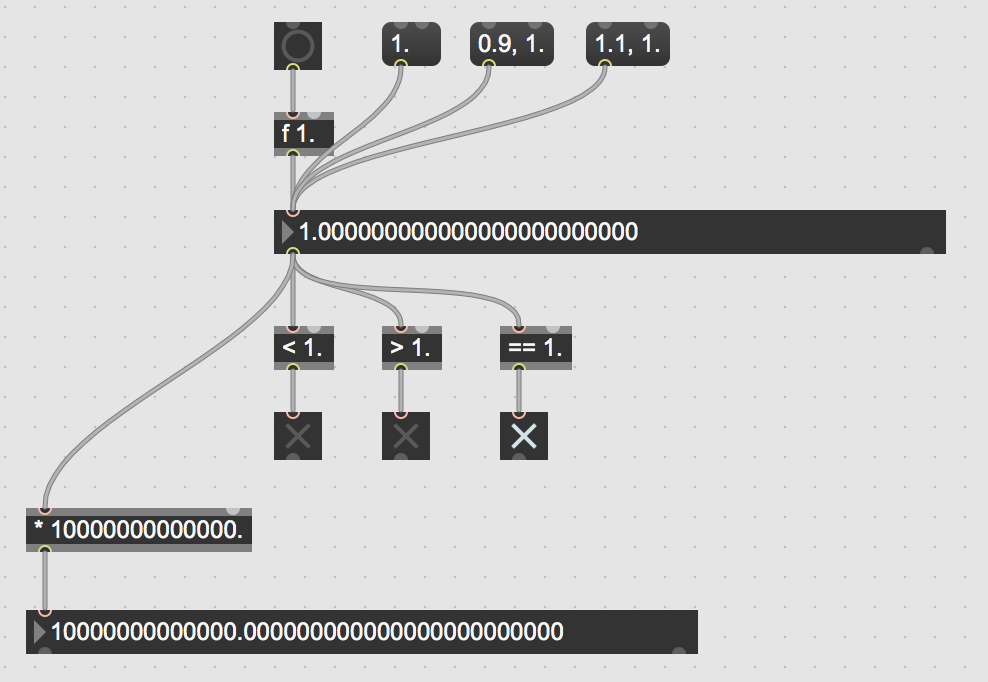
Also that gen~ patch above is likely hitting the exact same issue I mentioned regarding floating points being unable to accurately represent "0.1".
And if in that patch you click drag the float box from 0.99 to 1.? (edit)
@Roman I'm not sure I'm following what you were asking, but I tried to reproduce it, and here's the result. Floating points can't represent 1.01, or 0.01, so the result is quite possibly going to be not quite 1.0, although in this case, it actually is:

Ah, not available.
this is what flonum should do:
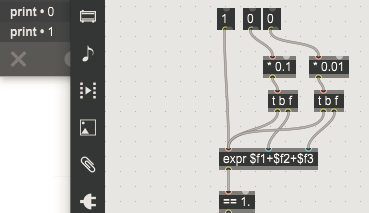
@David if you drag the float box, then you are performing a floating point addition with non-integer values, so it is likely to drift away from a precise value. Every little drag is adding (or subtracting) a small delta, depending on which decimal spot you drag upon.
@Roman I can't understand what that image is displaying. As I have said, floating point numbers cannot accurately represent 0.1 or 0.01, so any math using them could result in unexpected slight deviations (or, it might not, if you are lucky).
For fun, check out the same problems as they affect Javascript (https://javascriptwtf.com/wtf/floating-point-maths ), or indeed C++ (among the links I posted above).
BTW don't trust what [print] tells you. It limits the decimal precision by default, so it will round a number to the nearest decimal representation with a fixed number of digits. A number box with 24 digits (you can set that in the inspector for a flonum box) is more reliable to see what the actual value is. underlying
I think flonums by default have their "precision" set to 0, which will attempt to present a value on screen using a minimal number of digits. A number that is very close to 1. (like 1.00000000000000022204) will be displayed as "1.". Maybe that's the source of the confusion?
this is how it could also work.
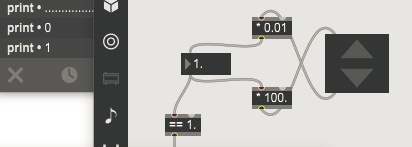
i fail to see why it does what it does and why it would be unavoidable.
sorry for the confusion graham i just changed my last two pictures and statements, please have a look again.
" @David if you drag the float box, then you are performing a floating point addition with non-integer values, so it is likely to drift away from a precise value"
that is totally clear. but why is the numberbox in float mode doing this?
dragging there should check which number is currently at that position and then add + 1 int.

In Max 6.1.9 (32bit) somehow the integer number can be click dragged to "precisely" from at least 6 places after the point. At least in the interface and also in the comparison the value represented seems to be more consistent?
@Roman the incdec example is doing the addition in integers (inside the incdec), not using floats. You're converting those to floats afterwards.
Clicking on incdec adds integer 1 to stored integer N, and outputs an integer. [* 0.01] converts that to a float, which loses precision (the number has a tiny offset from a multiple of 0.01 now, e.g. 1.01000000000000000000000888 etc.). This number is fed into a flonum, then to a * 100., which happens to result in a precise integer again (in the binary representation of the floats it is exactly the inverse of * 0.01 so that's not surprising). This integer goes back into incdec to do integer addition.
There's no accumulation of float error in this case because the operations are actually happening to integers.
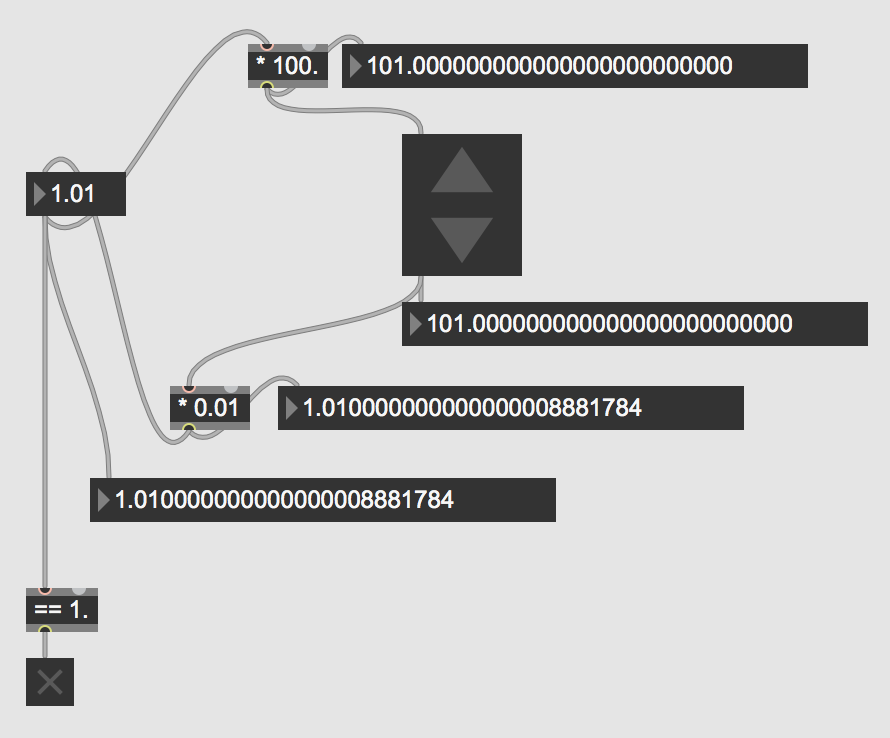
----
The problem with doing this kind of incdec-on-powers-of-ten operation on floats in general is that sometimes you actually do want the exact float value -- including whatever tiny far decimal place value it has -- not having it quantized to some larger decimal place. My guess is that this is the reason the flonum mouse interaction behaves as it does, rather than quantizing.
@David maybe this is down to a difference between 32-bit floats and 64-bit floats? I really don't know.
At least now the question is clear, that's probably very helpful for support now. E.g. "if I drag on a flonum in the 3rd decimal place, and I drag the number to the value 1.00, then the underlying number (what you see if you connect it to a flonum with 24 digits) the value should be 1.0000000000000000000000000 not 1.000000000000000000022204605". That makes sense, and I'd suggest passing that on in your chat with support.
i know why my example works, dont evade from the topic. we want flonum to work, too. :D
after all it is an interface element, not a teach-me-floating-point-tutorial.
people usually treat float numberboxes as if they were fixed point numbers. you enter 1-9 and you want 1-9. WYSIWYG, you know?
Perhaps it's an idea to have the same difference between the underlying value and the selected number in the flonum as the difference in the typed in argument in the comparator objects and its underlying value?
If the flonum is set to 0.0003 and the > object's argument typed to 0.0003, perhaps the underlying number can be the same, whether typed in or dragged to.
Precision balancing
Those grabs above are the outcome of dragging to 1.2 with the second decimal place.
The ones below are the outcome of typing.
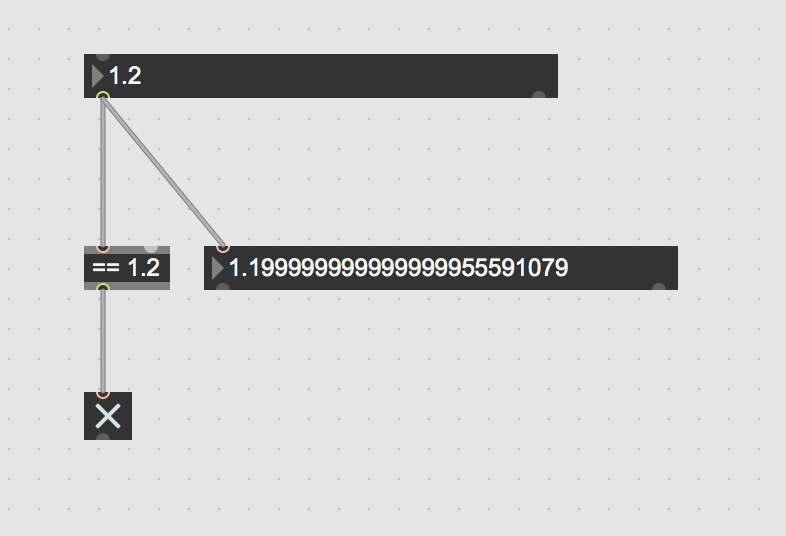
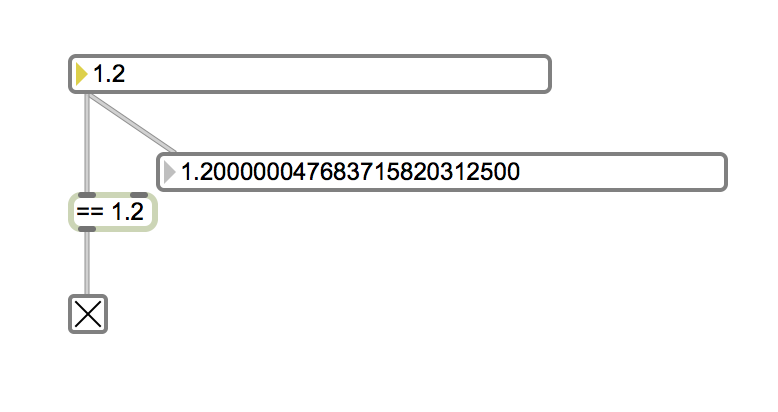
dont evade from the topic
😂 ...i don't think Graham was evading, he was helping deal with 'crossfire' here(many cooks in the kitchen can cause many different confusing tangents... i recall i created a frustrating occurrence of this for Andrew long ago when he was trying to explain something 😅)...
Graham's final answer: "suggest passing that on in your chat with support" seems best
(see bottom of this page: https://support.cycling74.com/hc/en-us/ )
Thanks Raja -- yes exactly, there were quite a few different points being raised in the thread (not all having to do with flonum -- e.g. the gen~ patch example being about floats not being able to represent 0.1) and floating point weirdness is a recurrent question and cause of confusion, so I thought it was a good idea to point out some useful resources in understanding them.
Honestly I was having trouble understanding what core problem was but now it's clear: when dragging on some decimal place in a flonum, the output should be the same as if that same number had been typed into the flonum (or a message box, or anything else really), which makes sense. That is, even though 1.2 can't be represented as a float, if the flonum is scrolled to 1.2 then the the output should be 1.19999999999999995559 (https://float.exposed/0x3ff3333333333333), just as it would be if you typed "1.2" into it. I suggest brining that to support as it is perhaps more clear?
I might be misunderstanding you Graham, but I think that the gen~ example shows the same problem of having different ways of inputting the same floating point value in the same UI object resulting in different values on its output.
I haven't heard back from Cycling support, but I included a link to this thread.
something i found most helpful reading this thread through, is that Graham noted about the difference between flonum display and others... and until this thread, i never realized number~ can't be set to display more than 9 decimal places in its inspector whereas flonum can display up to 52(i rarely use number~ unless i quickly want to snoop a general range something might fall at since there are so many samples it might miss displaying anyways in a changing signal)... what this tells me is that the gen~ example is actually irrelevant since the input even before gen~ is the problem... much of the wording in this thread and the examples given lead down a road that seems to confuse where the problem actually lies, specifically not with gen~ or <=~ objects... but just the UI itself... this is why it's confusing... you just need to connect number~ straight to flonum, or make sure flonum displays as many digits as possible and use that for input, and you'll see why it's confusing the way things have been 'tested' by patches so far:
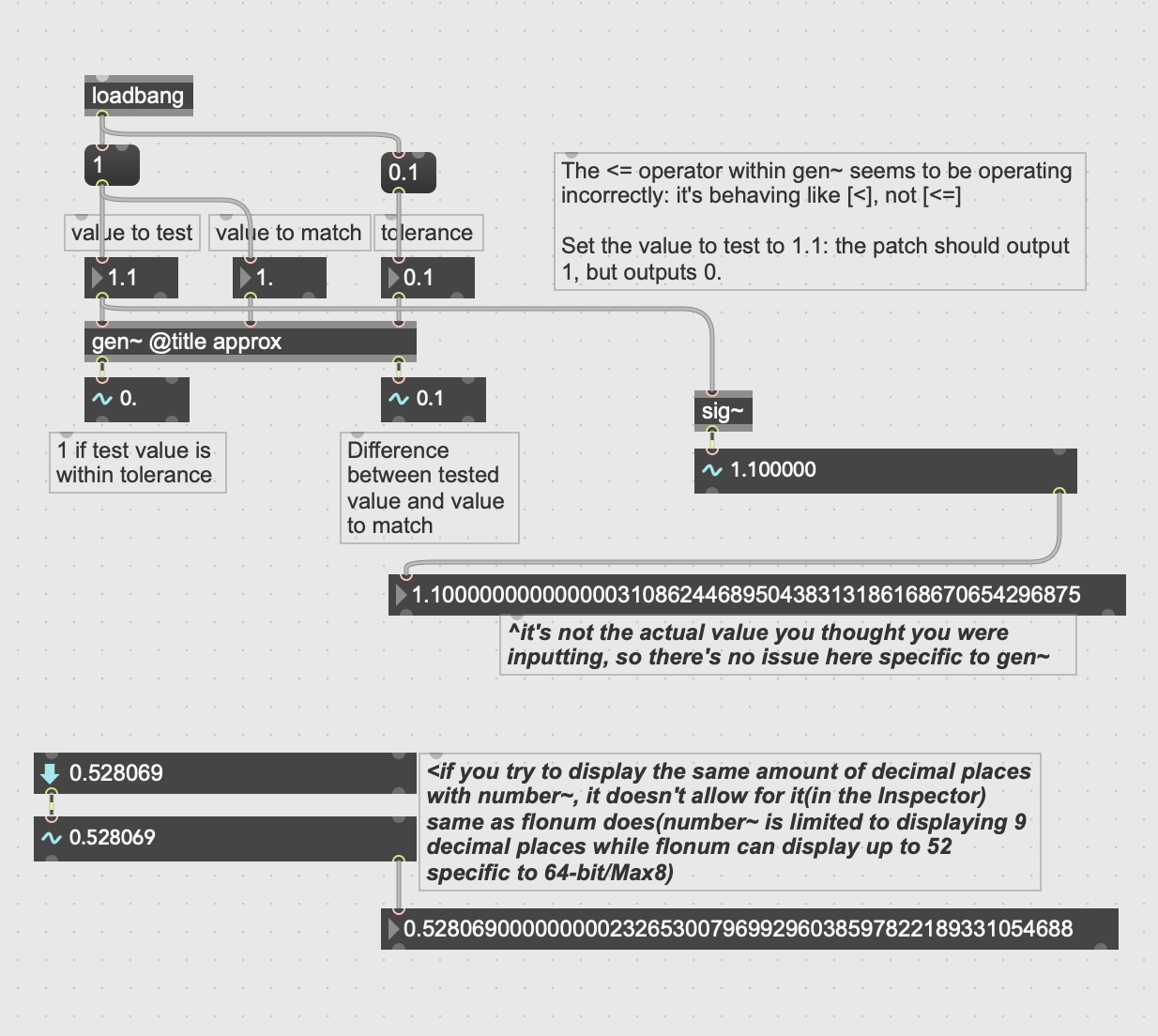
one small(😅) edit: if they add quantizing to the UI to output according to display resolution, that might also introduce a small overhead(not to mention the possibility of other inaccuracies which other users of legacy patches didn't expect)
i don't mean to go on about it, just adding this because while it might help support to see what you're actually referring to, it might also help you figure out a solution if you test with all the proper displays. hope it helps 🍻
(i promise this is my last comment here 😇 ...hoping not to confuse any further)
one other small edit(🤣): it is weird, though that number~'s inspector says 9 decimal places, but i think it's actually limited to '6'... just sayin'... ok now i'll stick to that promise for sure 👉🤐 .. 😁 😊 😇
I don't think quantising is the solution, more the consistent interpretation of floats with fewer decimal places
This is all very fascinating, explains my gen~ patch issue and also explains other oddities, like times I've got values like -0. instead of 0. for no discernible reason! Once explained, the reason for this apparently anomalous behaviour is clear, but I concur that there are elements of the UI that add to the confusion.
The gen~ patch I gave as an example above was built to recognise when a float comes into a certain range (a sort of "that's close enough"); I wonder if there's a use for an attribute for things like comparison objects that'd do much the same, but for very small tolerances. I.e. if the attribute is turned on, the object would look at an inputted number, and if it's within the margin of error created by how floating point numbers work, it'll treat it as if it's the nearest value specified to x number of decimal places. I.e., if it receives 1.000000000000000000022204605, it'll assume you meant 1.0000000000000000000000000000. If the attribute is turned off (default), it'll just behave as it has always behaved.
Oh and I meant to say, thank you Graham for taking the time to explain so thoroughly! I really appreciate it.
"Precision balancing"
that is yet another problem. not only that 32 bit allows other values than 64 bit, but you couldnt not count on max using 32 bit float precision correctly anyway.
Cycling support has replied that the flonum error has been reproduced and reported to the engineering team.
While looking through the Max documentation for coverage of float number precision and trying to see whether I missed an in depth explanation of the above discussed subjects there, whether to recommend an addition of such a thing to the documentation, I came across this for me unknown factor: "Floating point numbers can't exactly represent every number, sometimes a little fudge factor to account for this might be necessary" :-)
the mean thing about float formats is that you dont need it for most of the things you do with them.
until an audiofilter explodes or you have to deal with cos(exp(exp())) type of calculations.
or when you dont understand an object / there is a bug in an object.
Hey Graham, how does genExpr function 'int()' work in the context of float accuracy?
@Asher the same way C does.
The [int] operator (or int() function in genexpr) simply performs a static cast from the input from a double (a double-precision = 64-bit floating point number) to an int, and sends that on. Other operators below it might cast it back to double (e.g. if you send the output of [int] into [log]).
If the input to [int] was already integer type, no cast is performed.
If the input to [int] was a double with an integer value (e.g. 1.00000000000000), the cast (to int 1) will be performed, as in machine code these numbers have different binary representations.
In casting, C normally performs the same operation as [trunc], which rounds numbers toward zero. So 1.0001 and 1.9999 will both be cast to 1, and -1.0001 and -1.9999 will be cast to -1. So, gen [int] does the same. Use [round], [ceil], [wrap] etc. if you want different behviours.
TL;DR: gen [int] is the same as C: ((int)x)