Weird delay behavior in gen~
Hi
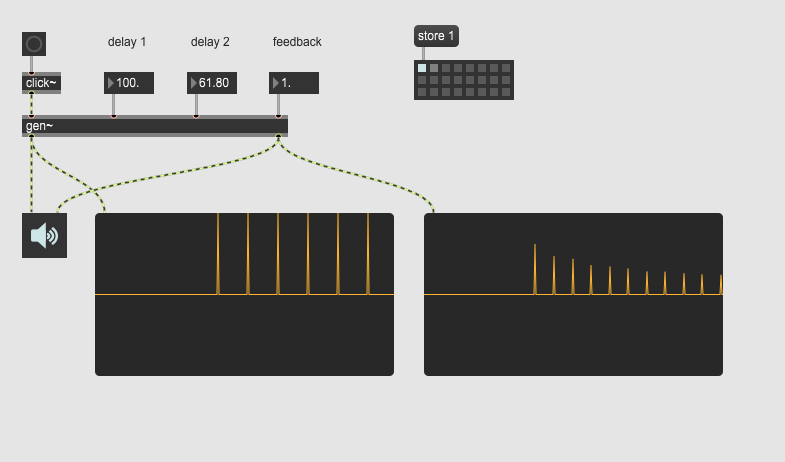
i've just noticed something weird when using more than one delay in a gen~ patcher (see the example below)
With a feedback value of 1, there should be no decay but this is only the case for the first delay, not the second one... unless the delay times are multiples of each other !
Is this a bug or am i doing something wrong ?
Thanks by advance
i'm getting the expected behavior, even with negative feedback:
not sure why your system would behave differently(?)
Thks for taking a look at it
In your video you are using preset 2 which is indeed working as expected (delay2 multiple of delay1)
Could you please try preset 1 ?
This is what i get
interesting, i've not used 'delay' enough in gen~(been using 'data' op with 'sample' and 'poke' for similar), seems like there is a phase-cancellation issue happening:
-you can switch the timing of the delays so that delay1 is at 61.8 and delay2 is at 100ms, and delay1 will respond similarly as delay2 does with your preset1(where delay1 is 100ms and delay2 is 61.8), but choose something like a relationship of 100ms to 150ms between them and they work as expected
-i tried adding "@feedback 1" to the delay op, it doesn't seem to make a difference either(but i wonder if maybe a delay of one-sample, which is what 'delay' implements to create feedback loops, might be causing this phase-cancellation - correction: i tried to add "@feedback 0" and it posts an error message saying there's a feedback loop that won't allow that, so this means it does it automagically and we don't even need to write that attribute, so with your patch there is definitely an added sample of delay on top of whatever you enter for the delay times)
-you can also tell it's a phase-cancellation because with infinite feedback, the phase-cancelled signal (whether delay1 or delay2), takes a very long time to die down all the way to 0... it's more like a gradual low-pass filtered effect smoothing out the clicks more and more over time
-i am a little confused as to why a value of 100ms allows that particular delay to work at infinite feedback no matter what(that is to say, it is not just a matter of having a whole number ratio between the two, you can try delay1 with a value of 64ms and delay2 at 128ms and they both die down in a gradually low-passed way) -> this issue may be tied to sample-rate somehow?
in any case, the way in which the signal dies down to my ears(especially with 64ms and 128ms as the delay times), sounds very much like creating a one-pole lowpass filter where a single-sample history is mixed in with the current sample, see the documentation here(if you option/alt-click on the gen~ op, to read its description), it says there's a delay of one-sample added, so i think this might be inadvertently low-pass filtering your feedback loop:

i'm not sure what to do about that(this doesn't seem like the intended behavior of delay? but then again, a real-life signal which is not perfectly asymmetrical might not get low-pass filtered so predictably? hmmm... i am indeed confused about this 😵💫)
i hereby approve the thread title, this is indeed a "weird" delay behavior in gen~😂
oh, i see now: switch sample-rate to 48kHz, and you can use 64ms and 128ms easily to get the expected result.
So the floating-point truncation of something like 68.1ms(multiplied by 44.1 samples per millisecond when using 44.1kHz sample-rate = 3003.21 samples), adds to that one-sample of delay which the 'delay' op implements for feedback loops, to probably create a more drastic low-pass filtering than just one sample of delay alone. this low-pass filtering is basically all that's happening here, i'm not sure what you could do about that, other than roll your own using "+="/"accum" or "phasor" for the indexing, and then 'sample', 'data', and 'poke' for all the rest.
Hi,
The reason is because of interpolation.
Internally, a delay line is just a series of samples, like a buffer~. If you want a 10 sample delay, then what is output is the sample that was input 10 samples ago, the 10th sample back from the current position. But let's say you want a 10.5 sample delay. There's no 10.5th sample. By default, what the delay operator does is linear interpolation: a weighted blend between the 10th and 11th samples. This is an attempt to guess what the signal would have been 10.5 samples ago (even though there is no actual data there). At 44.1kHz, a 100ms delay is 4410 samples ago. So it pulls out the 4410th sample. But a 61.8ms delay is 2725.38 samples ago. So again, the delay operator has to use interpolation to "guess" what the signal should be there, by a weighted mix of the values at 2725 samples ago and 2726 samples ago.
The trouble is, linear interpolation is not perfect, it tends to under- or over-estimate the signal slightly, and this manifests as the sound getting slightly duller and quieter. It's not usually very noticeable, but in a feedback loop this becomes much more apparent.
There are other interpolation modes you can try, like delay @interp cubic or delay @interp spline, but all of them are approximations, and they all have some filtering effect. Other methods of interpolation, such as allpass interpolation, may have phase distortion effects. No method is perfect. A sinc interpolation is usually about the best, but still limited by the size of the window, which also has a filtering effect. (There's an example of sinc interpolation for buffer playback in the gen~ examples folder, and a few more examples in the GO book of both sinc and allpass interpolation.)
Or, you can just disable interpolation altogether, using delay @interp none, and with that the feedback will be perfect. But, your delay times will always be an integer number of samples in length. Whether that matters depends on what you are using the delay for.
Graham
If i round the delay time in samples to the nearest int, it works as expected, indeed
Should have figured that out by myself really...
Thanks for your explanations though, very helpful
