Husserl Tutorial Series(1). Designing a good LFO in gen~ codebox
I get alot of questions about codebox, so before releasing Husserl3 I am writing a tutorial series describing, first, oscillators. Most of what I describe will be applicable to virtually any gen~ design, but at least I can make it more interesting by providing something you might actually want anyway, in what otherwise might be very dry reading. So this tutorial describes how to make a very efficient, simple, multiple-waveform LFO, with particular reference to optimizing conditional tests, function calls, and a little-known pipeline optimization technique based on vector optimization for supercomputers. Later I will be posting a brief version of my popular prior blogs on interpolation for wavetables, and on anti-aliased oscillators. Tutorials in this series:
Designing a good LFO in gen~ Codebox: https://cycling74.com/forums/gen~-codebox-tutorial-oscillators-part-one
Resampling: when Average is Better: https://cycling74.com/forums/gen~-codebox-tutorial-oscillators-part-2
Wavetables and Wavesets: https://cycling74.com/forums/gen~-codebox-tutorial-oscillators-part-3
Anti-Aliasing Oscillators: https://cycling74.com/forums/husserl-tutorial-series-part-4-anti-aliasing-oscillators
Implementing Multiphony in Max: https://cycling74.com/forums/implementing-multiphony-in-max
Envelope Followers, Limiters, and Compressors: https://cycling74.com/forums/husserl-tutorial-series-part-6-envelope-followers-limiting-and-compression
Repeating ADSR Envelope in gen~: https://cycling74.com/forums/husserl-tutorials-part-7-repeating-adsr-envelope-in-gen~
JavaScript: the Oddest Programming Language: https://cycling74.com/forums/husserl-tutorial-series-javascript-part-one
JavaScript for the UI, and JSUI:<a href="https://cycling74.com/forums/husserl-tutorial-9-javascript-for-the-ui-and-jsui"> https://cycling74.com/forums/husserl-tutorial-9-javascript-for-the-ui-and-jsui
Programming pattrstorage with JavaScript: https://cycling74.com/forums/husserl-tutorial-series-programming-pattrstorage-with-javascript
Applying gen to MIDI and real-world cases. https://cycling74.com/forums/husserl-tutorial-series-11-applying-gen-to-midi-and-real-world-cases
Custom Voice Allocation. https://cycling74.com/forums/husserl-tutorial-series-12-custom-voice-allocation
Designing the Perfect LFO
Even for an LFO, codebox is more efficient than wired design because it allows for conditional tests, whence CPU-intensive operations can be skipped if not needed. Typically, there is a huge amount of stuff you don't need to do every clock cycle. Indeed, after reading enthusiastic propaganda for programming your own branches and loops, one might assume conditional tests provide a complete and worry-free solution
Pipelining and Branching
However, audio routines that run purely 64-bit floating-point calculations must pipeline everything through the microprocessor's 'FPU' ('floating-point unit'). Unlike simple integer operations, floating-point execution almost always takes more than a few clock cycles to do anything. While you can't do better in terms of quality, unnecessary calculations can really bog down your design. But well-designed floating-point code can be almost as efficient as integer code, as long as one remembers the results of any one operation aren't available right away. There is a corollary benefit that the integer unit isn't being used at all, so the processor can run another 'thread' on the integer unit concurrently.
In both integer and floating-point code, it's important to be careful with making conditional tests, because they can cause the longest stalls in the CPU pipeline throughput, while the condition is being evaluated. To increase processor clock speeds, engineers have deepened and extended the pipelines throughout the CPU, particularly for instruction prefetch and address lookup, both of which incur longer delays waiting for memory access. Pipeline stalls add incrementally, so the faster one's CPU, the faster one's code will become if you design it to minimize pipeline stalls.
This diagram of the Pentium pipeline rather stupidly doesn't show the FPU<->data cache connection as bidirectional, which is a copy of my original mistake I'd really forgotten about and didn't think I'd be reminded of again 25 years later (my original had different arrowheads, so it's not mine, but seeing people are still copying my mistakes 25 years later makes me cringe). My manager kindly said there isn't really any connection in the Pentium which is not bidirectional at this level of abstraction, so to some extent it's a matter of discretion. I still think it was a stupid mistake, and I'm rather amused it was redrawn, probably by someone else working for her, because she thought my arrowheads were too dainty for Intel's cheap manual printing to capture. Seems she was right about that. Here it is, warts and all:
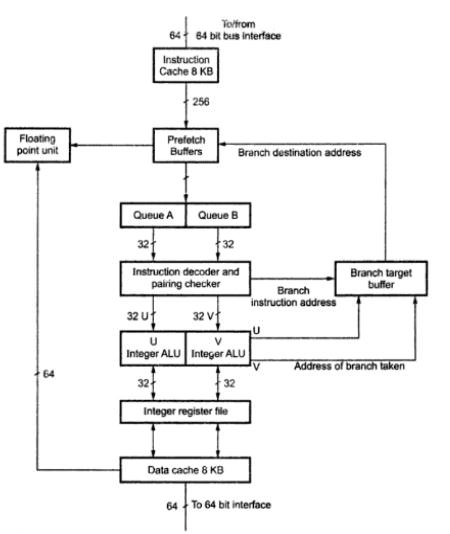
The 'branch target buffer,' which stores instruction addresses of conditional branches until the condition is decided, stalls floating-point code more than integer code, because floating-point operations almost always take longer to evaluate. ALSO, any conditional branch stalls the FPU, even if it is on the integer unit running on another thread. So the actual latency of all fPU operations is genuinely...unpredictable. This was an important cost-saving measure in the Pentium which normally doesn't impact performance so much because branches and floating-point calculations are typically not the most frequent of all possible machine instructions.
Optimizing for Failed Conditions
Designers of the most recent and most expensive CPUs try to evaluate both sides of a binary code branch in parallel, then discard one side of the branch code, to reduce pipeline stalls. But that old supercomputer technique still has disadvantages in cache and processor resource consumption. Moreover, most programs besides weather forecasting and analog simulations don't use floating-point exclusively, so except for geniuses looking for planets orbiting black holes in other galaxies, most people will find it exorbitantly expensive.
All desktop and laptop CPUs in current usage accelerate processing by expecting the conditional test to fail, because that is the most common result of conditions in loop tests. Thus they start evaluating code assuming a negative result while the condition is still being evaluated, then discard that processing if the conditional test proves to have a positive result instead. There was some debate, once upon a time, about whether the processor would be better doing other things, but proof of the unexpectedly large benefit of false-branch execution was my tiny contribution to the Pentium I's superscalar architecture when I worked for Intel way back in 1994. The technique proved to be the design's greatest performance improvement over the 80486, and aside from cost-optimized notepads and phones, it has become a standard implementation in all modern general-purpose CPU architectures. Because microprocessors still have trouble doing much better than false-branch predictive preprocessing, it is good practice to put the code for the most commonly expected results of a test in its false, or failure, branch, as I will illustrate in the second ramp generator example below.
The Simplest Possible Ramp Generator
Almost all oscillators start with a zero-to-one ramp generator, the simplest of which can avoid a conditional test altogether. The best way not to stall your pipeline is not to give it reason to stall! Like this:
History ramp;
ramp = fract( ramp + freq/samplerate );In practice the division, [1/samplerate], is best precalculated to remove a CPU-expensive division operation, so it becomes
Param freq, rsr;
History ramp1;
ramp1 = fract( ramp1 + freq*rsr );where rsr is 1/samplerate. Also, if possible, the frequency should usually be multiplied by 1/samplerate in advance, because it otherwise is recalculated every clock cycle. Even on modern CPUs, floating-point divisions typically take about 20 times longer than floating-point multiplies, and about 40 times longer than floating-point adds. It's still pipelined, but it's best to avoid divisions whenever possible.
Optimizing Params
Params aren't evaluated as frequently as other code in codebox. The exact rate is probably based on your audio-driver configuration, although I was once told it was every 256 clock cycles. Params also can't be changed in codebox, so they can't occur on the left side of a statement. But if the param is combined with standard variables or History operators on the right side of a code statement, it has to be evaluated every single clock pass. Hence, however much this might look stupid to a less knowledgeable programmer, the [freq*rsr] calculation should be on a separate line, to achieve maximal performance:
Param freq, rsr;
History ramp1;
inc = freq*rsr;
ramp1 = fract(ramp1 + inc);Now this ramp generator could hardly be a simpler floating-point operation, because if you precalculate the step increment, it only needs one floating-point add, after which the mantissa is kept and the exponent discarded, one of the few single-clock operations in the FPU universe. There are also a number of more sophisticated built-in methods which one could use in Max, but the above code does not require setting any function options, each of which introduce a branch test, and this little code trick with the float() operator obviates the need for any branch test at all!
For sync oscillators, the ramp needs to be reset on a trigger signal, typically, on the rising edge of an envelope gate signal. Other audio-rate oscillators, LFOs, and sample&hold circuits are typical sources for sync signals. Here a conditional test cannot be avoided, but it still can be very efficient in codebox:
Param freq, rsr;
History ramp2;
in1 = gate;
inc= freq * rsr;
trigger = change(gate) >0;
ramp2 = (trigger)? 0 : fract(ramp2 + inc);Again this hardly requires a dedicated method, and the above ternary operation to determine if the ramp should be reset is also one of the most efficient CPU operations, because it is a binary condition with the result operand already called before the condition is evaluated. This allows the CPU prefetch mechanism to preload the operand, in this case a static variable, while the condition is being evaluated, and still use it regardless the condition's outcome. If there isn't a sync signal, the processor has already assumed a false result and started evaluating the ramp, so the sync ramp causes absolutely zero performance penalty, aside from a few extra instructions for the conditional branch and constant, compared to the first example. Ternary operators are thus the most desirable form of all conditional tests. As noted above, the first part evaluated in a ternary test should be the least-frequent result, so as the trigger is relatively rare, the reset to zero should precede the more frequently expected ramp-value calculation.
A Multiple-Waveform LFO
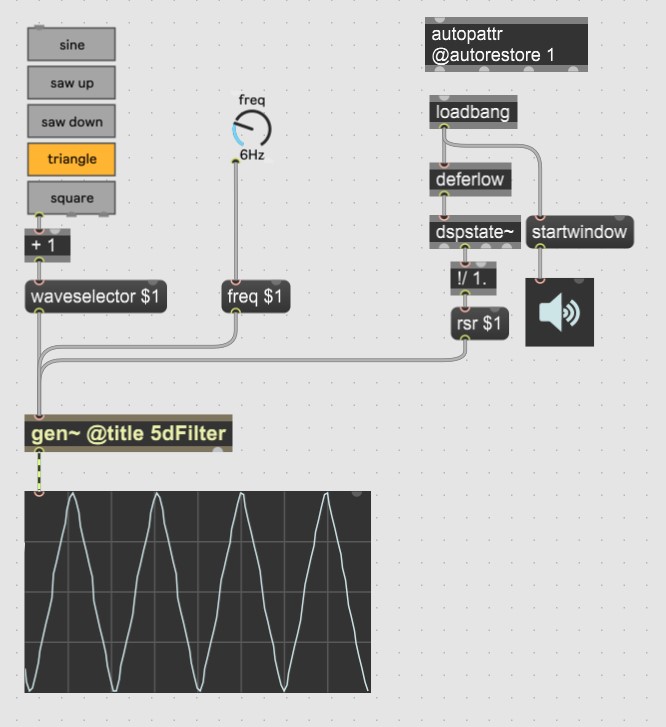
Max contains a built-in function for evaluation of conditions called [selector()}. This allows for selection of different waveforms, as in the following example from Husserl for its simplest LFO. It takes the above ramp generator's output and 'shapes' it to the standard sine, saw, and square waves:
Param freq, waveselector, rsr;
History ramp3;
inc = freq *rsr;
ramp3 = fract(ramp3 +inc);
out1 = selector(waveselector,
cycle(ramp3, index="phase"), // sine oscillator
ramp3 *2 -1, // rising saw
ramp3 *-2 +1, // falling saw
triangle(ramp3) *2 -1, // triangle
(ramp3 >.5) *2 -1 // square
);
By putting the different waveshape inside a selector clause, only the operations needed for that waveform are performed on each cycle. Like the ternary operator, the selector clause is more efficient than [if..then] statements, in this case because the term for the condition is declared only once.
Here's a demo download. The scope display looks a little funky due to averaging a lot of samples for each point, and fixing that kind of thing will be in the next tutorial series.
Note: after sharing the above, I noticed the peek, cycle, and other such buffer access methods in gen~ return two values by default, unless only one value is explicitly defined for their return. So to improve on the above perfect example already, lol, the cycle~ call should be in a user-defined function:
Function mysine(ramp){
x = cycle(famp, index = "phase");
return x;
}
Param freq, waveselector, rsr;
History ramp3;
inc = freq *rsr;
ramp3 = fract(ramp3 +inc);
out1 = selector(waveselector,
mysine(ramp3, // sine oscillator
ramp3 *2 -1, // rising saw
ramp3 *-2 +1, // falling saw
triangle(ramp3) *2 -1, // triangle
(ramp3 >.5) *2 -1 // square
);
You will see the difference between the two above code examples by looking in the gen~ 'code window,' labeled with a 'C' in the inspector sidebar.
Optimal Function Usage: Frequency, Arguments, and Returns
The above selector clause uses gen~'s [cycle()) function for the sine waveshape. [cycle()] performs sample lookup in a precalculated table of sine values rather than one of the most CPU-intensive operations of all, loosely referred all together as 'transcendentals,' which can take more than four times longer than divides (other operations in this category include logs and exponentials). It does add one conditional branch test for the value of the index operator, and my next tutorial will describe how to remove that too if you want.
The above example also uses gen~'s built-in triangle function. Generally speaking, if built-in functions do not contain options, one can rely on them as being as efficient as native code. This is because, in object-oriented environments, programmers typically write more than one routine for a single method, one of which contains no options, and others of which evaluate the options. Then when the compiler builds the binaries, it substitutes a call to the specific required version of a method, depending on the specific arguments there are in the user's function call.
Hence the sine oscillator in the above example could be marginally more efficient by removing the need to evaluate its 'index' attribute. But it's safe to assume Cycling74 has written an optimal version of the triangle function, so it's probably as fast as inline code outside its creation of a register window to pass the variables in and out of the function, the overhead of which is virtually nothing in modern CPUs. The number of arguments and returns do make a difference, but it's something you probably will only encounter in your own code. For example, in the above selector statement, most of the calculations are with constants, and it only contains two variables: one upon which the waveform is chosen, and the other of which is the current value of the ramp; and it returns one variable, the current value of the LFO. That easily fits in Intel's meager count of four data registers.
Functions with more than four arguments, or more than four returns, do cause significant performance degradation on the x86 architecture, because the extra data has to be pushed and pulled on the data stack. That's why most functions have four arguments or less. Notwithstanding, if you use the same function multiple times, you also reduce instruction-cache load by using functions instead of inline code. So even functions with larger numbers of arguments or returns can have performance benefits. But in most cases, it's best to keep the arguments and returns to four or less.
There's STILL such a thing as TOO MANY Function Calls...
Another frequently cited benefit of function calls is that they can remove variables from the main routine, so some programmers fill their code with function calls absolutely everywhere. Programmers usually think of it as a coding convenience, and function calls also do improve data caching somewhat, within limits. But there are real limits to the number of function calls you should use, because the address lookup for the function call also imposes a load on something called the 'translation lookaside buffer' (TLB), which keeps recently used virtual-to-physical memory mappings. The TLB is large and expensive, so it's severely more limited than instruction and data caches--another fact that CPU manufacturers tend to hide for competitive reasons. But the TLB probably has more effect on CPU performance than instruction/data caches these days, even though cache size is usually the most cited number after clock speed.
TLBs only have between 32 and 256 entries in most current products. Mostly, only 32. Hence it is good performance practice to limit function calls in execution bodies to a few dozen that you use more frequently, if possible--Although for choices like different oscillator waveforms, only one of the functions are routinely called, and that means, functions within user-selected conditions are a good thing, because they remove instructions from the regularly-called main code body.
Vector Optimization: Interleaving Code Routines
Looking at this example again:
// this is an infrequent param evaluation:
inc = freq *rsr;
// this takes a couple of clock cycles:
ramp3 = fract(ramp3 +inc);
//this takes a long time:
osc = selector(waveselector,
cycle(ramp3, index="phase"), // sine oscillator
ramp3 *2 -1, // rising saw
ramp3 *-2 +1, // falling saw
triangle(ramp3) *2 -1, // triangle
(ramp3 >.5) *2 -1 // square
);
// so put other other stuff here...
out1 = osc;So the param statement only gets evaluated infrequently, and the ramp is faster as a result. But It will take the CPU some time to evaluate the selector statement, during which the variable "osc1" won't be available yet. So if you have other stuff to do, it's good practice to put that immediately after the selector clause. That's just a specific example of the general paradigm of 'vector optimization' that applies throughout floating-point optimization. That is, originally this was an optimization for supercomputer vector units performing array processing, but it applies just as much to any code optimization for pipelined instructions. You could think of it as instructions 'vectoring' through the FPU pipeline, but more properly these days, the technique is called 'functional interleaving.' For example, you might want two LFOs:
lfo(inc, waveselector){
History ramp;
ramp = fract(ramp +inc);
return selector(waveselector,
cycle(ramp, index="phase"), // sine oscillator
ramp *2 -1, // rising saw
ramp *-2 +1, // falling saw
triangle(ramp) *2 -1, // triangle
(ramp >.5) *2 -1 // square
);
}
Param freq1, freq2, waveselector1, waveselector2, rsr;
inc1 = freq1 *rsr;
out1 = in1;
inc2 = freq2 *rsr;
osc1 = lfo(inc1, waveselector1);
osc2 = lfo(inc2, waveselector2);
out1 += osc1;
out1 += osc2;Because each line in the code body doesn't need the result of the previous one, the CPU doesn't need to wait for its result before continuing to process the routine. It's a little counterintuitive, because one naturally wants to group code lines for the same function together. But interleaving routines in your code is the next most significant way you can yourself directly influence the number of pipeline stalls in your code design structure.
Interleaving makes the most difference when your audio driver is set to short sample windows, because Max can still interleave processing itself when the results of one clock cycle don't affect the next, in many cases. But not in this case. Oscillators need to recalculate the ramp every single clock cycle, and the result of the History operator from the previous pass is needed in the very next audio clock cycle. So maybe someone from Cycling74 could recommend a way to attain better performance from precalculating the ramp as an array batch in MC and passing the results in from a buffer...but maybe not. Then one has a loss in performance from the interface exchange. So it's still likely not to be much faster than interleaving your own code anyway.
Unrolling Loops
All of the above applies equally to "if..then" statements, "while" loops, and "for" loops. There is one final topic on loops: "loop unrolling." In past days, compilers provided an option to "unroll" loops by creating one long routine containing each of the loops "spelled out" as it were, to remove the branch and conditional test at each loop iteration. Back in the 1990s there was extensive debate on whether loop unrolling actually improves performance, as it also increases cache load, and it still goes back and forth, as cache sizes increase, whether loop unrolling might again be a better idea than it was for a while, but the jury is still out on it.
It is an option on better compilers for them to unroll loops automatically, but one can safely assume programmers don't enable it. In some cases, one might want to unroll loops manually. Coders overwhelmingly shun that practice, as it's more to maintain, but for VERY short loops of two or three iterations, it unquestionably results in faster code.
Conclusion
Thank you for reading my little tutorial. There will be a bit more on code optimization in the next two tutorials. Happy patching everyone )
Appendix:
thx!!!
This turned out to be my most popular share on Facebook this year. It has 54 likes already in the gen~ group alone, which isn't even as large as the cmax group. Perhaps I should share it on KVR code developers or something.
Hi Ernest, I'd like to e-mail you for regular lessons to help optimise the signal of my patch www.liveloop.live.
I know this is not the right place to connect with you but I couldn't find your e-mail. You can connect with my to josep@liveloop.live and remove this message.
Thank you
HI Josep, I'm going to be kind of busy with my own project for a while. It's probably going to take me until April to finish Husserl 4, because after I get the multichannel portin done, I'll finally be porting my Reaktor metasequencer to Max. If you still need some help after that's done I'll be glad to donate some work to your own project :)
Metaseq~!!
The metasequencer will be relatively simple after getting multiphony working, lol. I already have a design in Reaktor, and I did a couple of trial ports of parts of it into Max already, so I think it might be done in the Spring. The 80-page user manual is also already done, on the yofiel blog here:
Excellent tutorial series, thanks a bunch.
Thank you for the explanations behind the code strategies. My ‘low level’ coding experience pre-dates the Pentium (8085 and Lattice C).
I’ll do a code review of my gen~ patches to squeeze more out of them.
Thanks Ernest your contributions are so incredibly valuable
This is really excellent. These explanations are very helpful.
There is one thing I am having trouble wrapping my head around in the last code example for the double LFO. I have modified the patch example above to use the double LFO code (just had to change the out's to use = instead of +=) and got everything working.
But then while studying it, I am surprised that both LFOs can (seemingly?) share the same History ramp variable inside the lfo() function. I would assume that with a single ramp, accessed in succession for each osc, they would interfere with each other, but the outputs I am getting confirm that there are two independent LFO signals (i.e., different frequencies and shapes).
That's because each call to the lfo function, actually a 'method' in object-oriented terminology, creates a new instance of the code in memory, so the history variable (actually called a 'static varible' in object-oriented terminology) is stored and recalled separately.
Thanks for that confirmation. That is not what I would have assumed, but it makes sense if there is a new copy/instance of the method in memory for each call to it in the code.
So if History variables in gen are (or, are like?) static variables, when scoped inside a function it seems they are static/shared across all invocations of/calls to the same copy of a method. That seems slightly different from a static variable on a class in which the value is shared across all instances of the class, which is how I was initially interpreting it.
well the scoping of variables in the main routine is similar to your latter statement, but the variables in the main routine are not meant to be global. One occasionaly encounters bugs with that, so it is wise to name every single variable uniquely.
Hi Ernest! Thank you for the series, it is just so great.
I have a question. When you say:
Functions with more than four arguments, or more than four returns, do cause significant performance degradation on the x86 architecture, because the extra data has to be pushed and pulled on the data stack. That's why most functions have four arguments or less.
What about x64? And is it also the same for gen~ patches with more than 4 inlets? (Sorry if I made a stupid question, I don't really have large knowledge on the matter)
Hi Paolo. The x64 architecture increases the data path to 64 bits, but otherwsie is essentially the same as x86, so the four operand limitation still exists. However the number of inlets dont make much difference.
Hello Ernest, thank you for this tutorial series, I am learning a lot! What are your opinions on using an if-branch to recalculate expensive calculations in gen and save them in a History variable like this:
Param freq;
History init(1), ramp, rsr;
// precalculate expensive division
if (init) {rsr = 1/samplerate; init = 0;}Also, what made you choose Max for your synthesizer instead of more text-based environments like CSound, Supercollider, Faust (...) or just straight C/C++ (since you obviously have a low-level programming background)?
Yes, I factor out and precalculate all division and transcendental constants I can in exactly the manner you illustrate.
With regards to other IDEs, I wanted something that would provide commercial support of cross platform binary compilation. It's transpired c74 hasnt had much luck at that. I'd say JUCE is definitely done far better.
